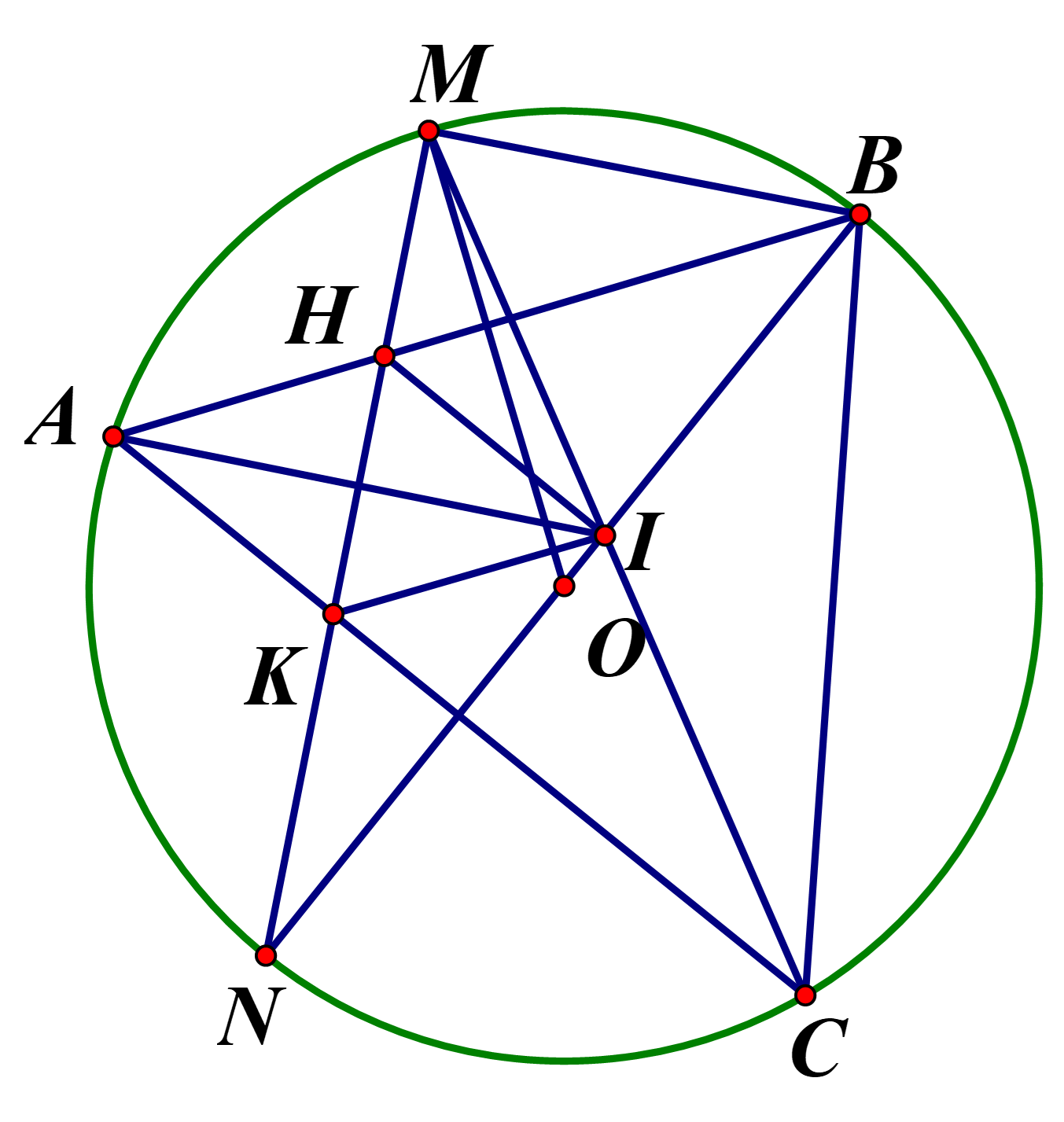
Cho đường tròn (O;R) với dây AB < 2R cố định Gọi C là điểm thuộc cung lớn AB sao cho ![]() nhọn ,Mvà N lần lược là điểm chính giữa cung nhỏ AB và cung nhỏ AC. Gọi I là giao của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K. Chứng minh rằng :
nhọn ,Mvà N lần lược là điểm chính giữa cung nhỏ AB và cung nhỏ AC. Gọi I là giao của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K. Chứng minh rằng :
1) Tứ giác BMHI nội tiếp.
2) NI.NB = NH.NM
3) KH là phân giác củ góc AKI, IA là phân giác của góc KIH
4) Khi điểm C di động trên cung lớn AB và thỏa mãn điều kiện đề bài thì tổng hai bán kính của hai đường tròn ngoại tiếp ![]() và
và ![]() có giá trị không đổi .
có giá trị không đổi .
 Giải bởi Vietjack
Giải bởi Vietjack
\( \Rightarrow \angle HMB + \angle HIB = 180^\circ \)mà \(\angle NIH + \angle HIB = 180^\circ \Rightarrow \angle HNB = \angle HIB\)
Xét \(\Delta NIH\)và \(\Delta NMB\)có: \(\angle MNB\)chung,
\( \Rightarrow \frac{{NI}}{{NM}} = \frac{{NH}}{{NB}} \Rightarrow NI.NB = NM.NH\)
\( \Rightarrow \angle KIN = \angle KCN\)(cùng chắn mà \(\angle KCN = \angle ABN\)(cùng chắn
\( \Rightarrow \angle KIN = \angle ABN\), mà chúng đồng vi \( \Rightarrow KI//AH\left( 1 \right)\)
Theo câu 1, tứ giác \(BHMI\)nội tiếp \( \Rightarrow \angle IMB = \angle IHB\)(cùng chắn
Mà \(\angle IMB = \angle CAB\), mà chúng đồng vị \( \Rightarrow IH//AK\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AHIK\)là hình bình hành
Lại có :
\( \Rightarrow \angle AKH = \angle AHK \Rightarrow \Delta AHK\)cân tại A\( \Rightarrow AH = AK\)
Hình bình hành \(AHIK\)có \(AN = AK \Rightarrow AHIK\)là hình thoi\( \Rightarrow KH\)là đường phân giác \(\angle AKI \Rightarrow IA\)là phân giác \(\angle KIH\)
\( \Rightarrow \Delta {O_1}AH\)cân tại \({O_1}\)và \(\Delta {O_2}BH\)cân tại \({O_2}\), có \(\angle A{O_1}H = 2\angle ANH\), \(\angle B{O_2}H = 2\angle BNH\)\( \Rightarrow \angle {A_1}OH = \angle B{O_2}H\)mà \(\angle ANH = \angle BNH\)
\( \Rightarrow \angle {O_1}AH = \angle {O_1}HA = \angle {O_2}HB = \angle O_2^{}BH\)
Gọi D là giao điểm của \(A{O_1}\)và \(B{O_2}\)có:
\(\Delta ADB\)cân tại \(D \Rightarrow M,O,D\)thẳng hàng
Có \(\angle AMD = \angle MAB = \angle ANM \Rightarrow MA\)là tiếp tuyến của \(\left( {{O_1}} \right) \Rightarrow \angle MAD = 90^\circ \)\( \Rightarrow MD\)là đường kính của \(\left( O \right) \Rightarrow D\)cố định
Ta chứng minh được : \(\angle A{O_1}H = \angle ADB \Rightarrow H{O_1}//D{O_2}\)
\( \Rightarrow \angle AOB = \angle H{O_2}B \Rightarrow H{O_2}//D{O_1}\)
Tứ giác \(H{O_1}D{O_2}\)là hình bình hành\( \Rightarrow {O_2}H = D{O_1}\)
Có \({R_1} + {R_2} = {O_1}A + {O_2}H = {O_1}A + {O_1}D = AD\)
\(A,D\)cố định \( \Rightarrow AD\)không đổi \( \Rightarrow {R_1} + {R_2}\)không đổi
Giải bài toán sau bằng cách lập hệ phương trình :
Để hoàn thành một công việc theo dự định thì cần một số công nhân làm trong một số ngày nhất định . Nếu tăng thêm 10 công nhân thì công việc hoàng thành sớm được 2 ngày. Nếu bớt đi 10 công nhân thì phải mất thêm 3 ngày nữa mới hoàn thành công việc. Hỏi theo dự định thì cần bao nhiêu công nhân và làm trong bao nhiêu ngày?
1) Giải hệ phương trình sau 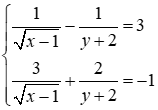
2) Cho Parabol ![]() và đường thẳng (d): y = 2x + 3
và đường thẳng (d): y = 2x + 3
a) Chứng minh rằng đường thẳng d cắt parabol (P) tại hai điểm phân biệt A, B và tìm tọa độ của A, B
b) Xác định điểm C thuộc cung nhỏ AB của parabol (P) sao cho diện tích ![]() lớn nhất .
lớn nhất .
Cho các biểu thức
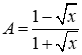 và
và 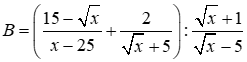 với
với ![]()
1)Tính giá trị của biểu thức A khi ![]()
2)Rút gọn B
3) Tìm a để phương trình A - B = a có nghiệm.