Cho hàm số \(y = f(x) = 2a{x^2}\)(với \(a\)là tham số). Kết luận nào sau đây là đúng ?
\(A.\)Hàm số \(f\left( x \right)\)đạt giá trị lớn nhất bằng \(0\)khi \(a < 0\)
\(B.\)Hàm số \(f\left( x \right)\)nghịch biến với mọi \(x < 0\,\,khi\,\,\,a > 0\)
\(C.\)Nếu \(f\left( { - 1} \right) = 1\)thì \(a = \frac{1}{2}\)
\(D.\)Hàm số \(f\left( x \right)\)đồng biến khi \(a > 0\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi Clà điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tùy ý trên cung CB ( D khác C, B). Các tia AC, AD cắt tia theo thứ tự là E, F
a) Chứng minh tam giác ABE vuông cân
b) Chứng minh FB2 = FD.FA
c) Chứng minh tứ giác CDFE nội tiếp được
a) Vẽ đồ thị hàm số
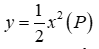
Cho phương trình \(2x - y = 5.\)Phương trình nào sau đây kết hợp với phương trình đã cho để được một hệ phương trình có vô số nghiệm ?
Cho phương trình x2 -mx + m - 1 = 0 (1)
a) Giải phương trình (1) với m = -2
b) Chứng tỏ phương trình (1) luôn có nghiệm x1, x2 với mọi giá trị của m
c) Tìm giá trị của m để (1) có 1 nghiệm bằng 3. Tìm nghiệm còn lại.
Một hình vuông có cạnh 6cm thì đường tròn ngoại tiếp hình vuông có bán kính bằng:
Trong mặt phẳng tọa độ Oxy, đồ thị các hàm số \(y = 2{x^2}\)và \(y = 3x - 1\)cắt nhau tại hai điểm có hoành độ là :