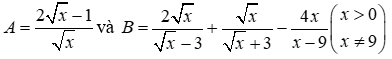Cho đường tròn tâm O đường kính AB. Điểm C bất kỳ trên nửa đường tròn (O) (C khác A và B). Kẻ đường kính CD của (O). Tiếp tuyến tại B của (O) cắt các tia AC, AD lần lượt tại M, N
1) Chứng minh tứ giác CDNM nội tiếp
2) Gọi H là trung điểm của BN, chứng minh O là trực tâm tam giác MAH
3) Kéo dài MO cắt AH tại K. Chứng minh:
a) OK.OM = OA2
b) K thuộc đường tròn đi qua 4 điểm M, C, D, N. Tính tỉ số
 Giải bởi Vietjack
Giải bởi Vietjack
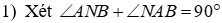
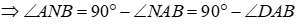
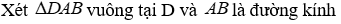
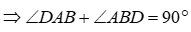
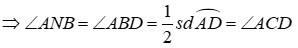
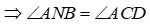
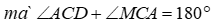
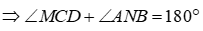
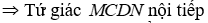
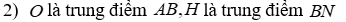
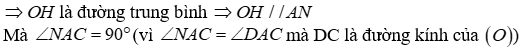
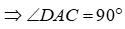
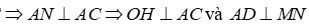
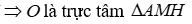
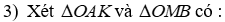
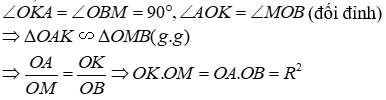
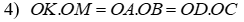

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình :
Hai vòi cùng chảy vào một bể không chứa nước thì sau giờ 40 phút sẽ đầy bể. Nếu chảy một mình thì vòi thứ hai chảy đầy bể nhanh hơn vòi thứ nhất là 3 giờ. Hỏi mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể ?
1) Giải hệ phương trình:
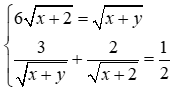
2) Cho đường thẳng (d): y = -2mx - m2 + 2m và parabol (P): y = x2
a) Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệr
Cho ba số thực a, b, c thỏa mãn đồng thời các điều kiện: a < b < x, a + b + c = 6; ab + bc + ca = 9
a) Chứng minh rằng a, c là hai nghiệm của phương trình bậc hai
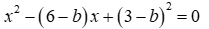
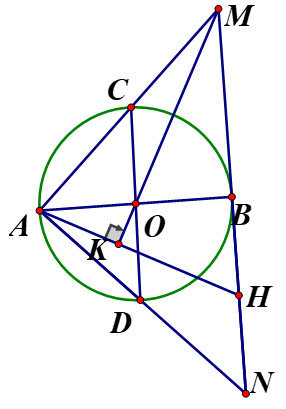
Cho biểu thức