Cho tam giác ABC vuông tại A có AC = 6 cm , \(\widehat {ACB} = 30^\circ \) . Vẽ đường tròn (O) đường kính AC cắt BC tại D, dây DE vuông góc với AC tại H
a) Tính BC
b) Chứng minh tam giác CDE đều
c) Qua B vẽ đường thẳng tiếp xúc với (O) tại M. Chứng minh tam giác BDM đồng dạng với tam giác BMC
d) Gọi K là hình chiếu vuông góc của H trên EC và I là trung điểm của HK. Chứng minh DK vuông CI
Giải bởi Vietjack
Lời giải
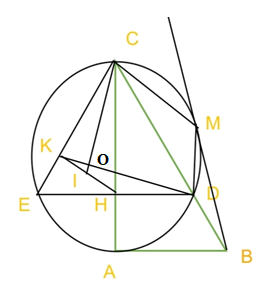
a) Xét tam giác ABC vuông tại A có \(\sin \widehat {ACB} = \frac{{AC}}{{BC}}\)
Suy ra \(\sin 30^\circ = \frac{6}{{BC}}\)
Suy ra BC = 6 . 2 = 12 (cm)
b) Xét đường tròn đường kính AC có DE ⊥ AC
Suy ra AC đi qua trung điểm của DE, H là trung điểm của DE
Xét tam giác ECD có CH vừa là đường cao vừa là đường trung tuyến
Suy ra tam giác ECD cân tại C và CH là tia phân giác của \(\widehat {EC{\rm{D}}}\)
Do đó \(\widehat {EC{\rm{D}}} = 2\widehat {ACB} = 2.30 = 60^\circ \)
Suy ra tam giác ECD đều
Vậy tam giác ECD đều
c) Xét đường tròn đường kính AC có \(\widehat {{\rm{BMD}}},\widehat {{\rm{MCD}}}\) là hai góc chắn cung MD
Suy ra \(\widehat {{\rm{BMD}}} = \widehat {{\rm{MCD}}}\)
Xét tam giác MDB và tam giác CMB có
\(\widehat {{\rm{BMD}}} = \widehat {{\rm{MCD}}}\) (chứng minh trên)
\(\widehat {{\rm{MBC}}}\) là góc chung
Suy ra tam giác BDM đồng dạng với tam giác BMC
Vậy tam giác BDM đồng dạng với tam giác BMC
d) Vì tam giác EHK vuông tại K
Nên \(\widehat {KEH} + \widehat {KHE} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {KHC} + \widehat {KHE} = \widehat {CHE} = 90^\circ \)
Suy ra \(\widehat {KEH} = \widehat {KHC}\)
Xét tam giác KEH và tam giác KHC có
\(\widehat {KEH} = \widehat {KHC}\) (chứng minh trên)
\(\widehat {EKH} = \widehat {HKC}\left( { = 90^\circ } \right)\)
Do đó (g.g)
Suy ra \(\frac{{KH}}{{HC}} = \frac{{EK}}{{EH}}\)
Suy ra \(\frac{{KH}}{{2HC}} = \frac{{EK}}{{2EH}}\)
Do đó \(\frac{{IH}}{{HC}} = \frac{{EK}}{{DE}}\)
Xét tam giác IHC và tam giác KED có
\(\frac{{IH}}{{HC}} = \frac{{EK}}{{DE}}\) (chứng minh trên)
\(\widehat {KED} = \widehat {IHC}\)(chứng minh trên)
Do đó (c.g.c)
Suy ra \(\widehat {KDE} = \widehat {ICH}\) (hai góc tương ứng)
Vì tam giác CHD vuông tại H
Nên \(\widehat {HC{\rm{D}}} + \widehat {HDC} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
\( \Leftrightarrow \widehat {HC{\rm{D}}} + \widehat {HDK} + \widehat {KDC} = 90^\circ \)
\( \Leftrightarrow \widehat {HC{\rm{D}}} + \widehat {ICH} + \widehat {KDC} = 90^\circ \)
\( \Leftrightarrow \widehat {IC{\rm{D}}} + \widehat {KDC} = 90^\circ \)
Gọi giao điểm của CI và KD là O
Xét tam giác OCD có \(\widehat {OC{\rm{D}}} + \widehat {ODC} + \widehat {DOC} = 180^\circ \)
Hay \(\widehat {DOC} = 180^\circ - 90^\circ = 90^\circ \)
Suy ra CI ⊥ DK
Vậy CI ⊥ DK.
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB với (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D.
a) Chứng minh tứ giác MAOB nội tiếp.
b) Gọi H là giao điểm của MO và AB. Chứng minh MC . MD = MA2. Từ đó suy ra MC . MD = MH . MO.
c) Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O).
Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \).
b) Tìm các điểm D, C sao cho\(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Cho đường tròn (O; R), đường kính AB. Kẻ tiếp tuyến Ax với đường tròn tại A. Lấy điểm M thuộc tia Ax, kẻ tiếp tuyến MC với đường tròn (O) tại C (C khác A). Tiếp tuyến của đường tròn tại B cắt AC tại D và cắt MC tại F. Nối OM cắt AC tại E
a) Chứng minh tứ giác OBDE nội tiếp.
b) Chứng minh AC. AD = 4R2.
c) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp ΔMOF.
Cho tam giác ABC cân ở A và H là trung điểm BC.Gọi I là hình chiếu vuông góc của H lên AC và O là trung điểm của HI. Chứng minh
a) \(\widehat {AHO} = \widehat {BCI}\)
b) AH . IC = HI . HC = HO . BC
c) Tam giác AHO đồng dạng tam giác BCI
d) AO vuông góc BI.
Cho tam giác ABC có \(\widehat A\) > 90°, kẻ AD vuông góc với AB, AD = AB (tia AD nằm giữa hai tia AB và AC), kẻ AE vuông góc với AC, AE = AC (tia AE nằm giữa hai tia AB, AC). Kẻ AH vuông góc với BC, AH kéo dài cắt DE tại M.
a) Chứng minh hai tam giác ABE; ADC bằng nhau và BE vuông góc với DC.
b) Từ D kẻ DP vuông góc với AM, từ E kẻ EQ vuông góc với AM. Chứng minh
DP = AH.
c) Chứng minh M là trung điểm của đoạn thẳng DE
d) Giả sử EQ = 3 cm; AQ = 4 cm. Từ Q hạ QI vuông góc với AE. Tính độ dài đoạn
thẳng AI; IE.
Cho đường tròn (O; R) đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao
điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE . CB = CI . CO.
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi
điểm C di chuyển trên Ax.
Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thỏa mãn các đẳng thức sau:
a) \(2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \)
b) \(2\overrightarrow {J{\rm{A}}} + \overrightarrow {JC} - \overrightarrow {JB} = \overrightarrow {CA} \)
c) \(\overrightarrow {{\rm{KA}}} + \overrightarrow {KB} + \overrightarrow {KC} = 2\overrightarrow {BC} \)
d) \(3\overrightarrow {{\rm{LA}}} + 2\overrightarrow {LC} - \overrightarrow {LB} = \overrightarrow 0 \)
Cho hai đường thẳng (d1): y = 2x + 5 và (d2): y = (m + 1)x + m – 1
Tìm m để hai đường thẳng cắt nhau tại điểm của tung độ bằng 1.
