Giải bởi Vietjack
Lời giải
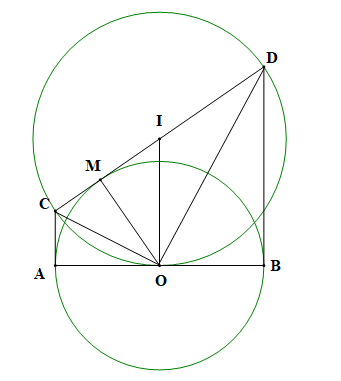
Vì CA ⊥ AB, BD ⊥ AB nên CA // BD
Suy ra ACDB là hình thang
Lại có \(\widehat {CAB} = 90^\circ \) nên ACDB là hình thang vuông
Đường tròn tâm I đường kín CD nên I là trung điểm của CD
Xét hình thang vuông ACDB có I là trung điểm của CD, O là trung điểm của AB
Suy ra IO là đường trung bình của hình thang
Do đó IO // CA
Mà CA ⊥ AB suy ra IO ⊥ AB (1)
Xét (O) có CA, CM là hai tiếp tuyến cắt nhau tại C
Suy ra OC là tia phân giác của \(\widehat {AOM}\)
Do đó \(\widehat {AOC} = \widehat {COM} = \frac{1}{2}\widehat {AOM}\)
Suy ra OD là tia phân giác của \(\widehat {BOM}\)
Do đó \(\widehat {BOD} = \widehat {DOM} = \frac{1}{2}\widehat {BOM}\)
Ta có \(\widehat {COD} = \widehat {COM} + \widehat {DOM} = \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.180^\circ = 90^\circ \)
Suy ra tam giác COD vuông tại O
Mà OI là đường trung tuyến
Do đó OI = \(\frac{1}{2}\) CD
Suy ra O thuộc (I) đường kính CD (2)
Từ (1) và (2) suy ra AB là tiếp tuyến của đường tròn (I)
Vậy AB là tiếp tuyến của đường tròn (I).
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB với (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D.
a) Chứng minh tứ giác MAOB nội tiếp.
b) Gọi H là giao điểm của MO và AB. Chứng minh MC . MD = MA2. Từ đó suy ra MC . MD = MH . MO.
c) Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O).
Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Cho tam giác ABC vuông tại A có AC = 6 cm , \(\widehat {ACB} = 30^\circ \) . Vẽ đường tròn (O) đường kính AC cắt BC tại D, dây DE vuông góc với AC tại H
a) Tính BC
b) Chứng minh tam giác CDE đều
c) Qua B vẽ đường thẳng tiếp xúc với (O) tại M. Chứng minh tam giác BDM đồng dạng với tam giác BMC
d) Gọi K là hình chiếu vuông góc của H trên EC và I là trung điểm của HK. Chứng minh DK vuông CI
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \).
b) Tìm các điểm D, C sao cho\(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Cho đường tròn (O; R), đường kính AB. Kẻ tiếp tuyến Ax với đường tròn tại A. Lấy điểm M thuộc tia Ax, kẻ tiếp tuyến MC với đường tròn (O) tại C (C khác A). Tiếp tuyến của đường tròn tại B cắt AC tại D và cắt MC tại F. Nối OM cắt AC tại E
a) Chứng minh tứ giác OBDE nội tiếp.
b) Chứng minh AC. AD = 4R2.
c) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp ΔMOF.
Cho tam giác ABC cân ở A và H là trung điểm BC.Gọi I là hình chiếu vuông góc của H lên AC và O là trung điểm của HI. Chứng minh
a) \(\widehat {AHO} = \widehat {BCI}\)
b) AH . IC = HI . HC = HO . BC
c) Tam giác AHO đồng dạng tam giác BCI
d) AO vuông góc BI.
Cho đường tròn (O; R) đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao
điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE . CB = CI . CO.
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi
điểm C di chuyển trên Ax.
Cho tam giác ABC có \(\widehat A\) > 90°, kẻ AD vuông góc với AB, AD = AB (tia AD nằm giữa hai tia AB và AC), kẻ AE vuông góc với AC, AE = AC (tia AE nằm giữa hai tia AB, AC). Kẻ AH vuông góc với BC, AH kéo dài cắt DE tại M.
a) Chứng minh hai tam giác ABE; ADC bằng nhau và BE vuông góc với DC.
b) Từ D kẻ DP vuông góc với AM, từ E kẻ EQ vuông góc với AM. Chứng minh
DP = AH.
c) Chứng minh M là trung điểm của đoạn thẳng DE
d) Giả sử EQ = 3 cm; AQ = 4 cm. Từ Q hạ QI vuông góc với AE. Tính độ dài đoạn
thẳng AI; IE.
Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thỏa mãn các đẳng thức sau:
a) \(2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \)
b) \(2\overrightarrow {J{\rm{A}}} + \overrightarrow {JC} - \overrightarrow {JB} = \overrightarrow {CA} \)
c) \(\overrightarrow {{\rm{KA}}} + \overrightarrow {KB} + \overrightarrow {KC} = 2\overrightarrow {BC} \)
d) \(3\overrightarrow {{\rm{LA}}} + 2\overrightarrow {LC} - \overrightarrow {LB} = \overrightarrow 0 \)
