Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh và SAEF = cos2A.SABC.
b) Gọi M là trung điểm của BC. Đường thẳng vuông góc với HM tại H cắt AB, AC lần lượt tại P và Q. Chứng minh PH = QH.
c) Chứng minh \(\cot A + \cot B + \cot C \ge \sqrt 3 \).
Giải bởi Vietjack
Lời giải
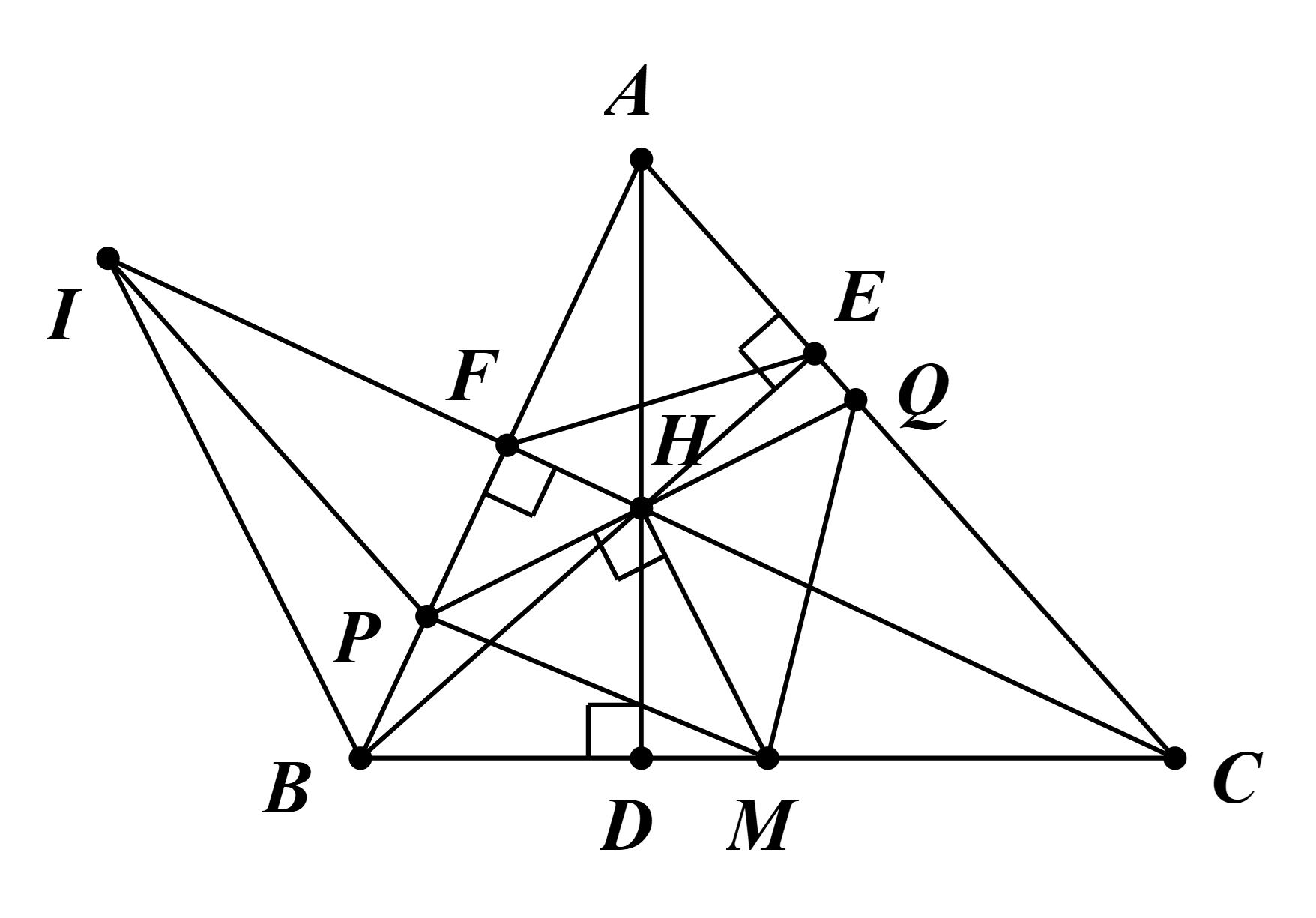
a) Xét ∆BAE và ∆CAF, có:
\(\widehat A\) chung;
\(\widehat {BEA} = \widehat {CFA} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\).
Xét ∆AEF và ∆ABC, có:
\(\widehat A\) chung;
\(\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\,\,\,\left( {do\,\,\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}} \right)\).
Do đó (c.g.c).
Ta có \(\frac{{{S_{AEB}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}AE.BE}}{{\frac{1}{2}AC.BE}} = \frac{{AE}}{{AC}}\).
Tương tự, ta có \(\frac{{{S_{AEF}}}}{{{S_{ABE}}}} = \frac{{AF}}{{AB}}\).
Suy ra \(\frac{{{S_{AEF}}}}{{{S_{ABE}}}}.\frac{{{S_{AEB}}}}{{{S_{ABC}}}} = \frac{{AF}}{{AB}}.\frac{{AE}}{{AC}} \Leftrightarrow \frac{{{S_{AEF}}}}{{{S_{ABC}}}} = \frac{{AE}}{{AB}}.\frac{{AF}}{{AC}} = \cos A.\cos A = {\cos ^2}A\).
Vậy SAEF = cos2A.SABC.
b) Gọi I là điểm đối xứng của C qua H. Suy ra HC = HI.
Ta có M là trung điểm BC và H và trung điểm CI.
Suy ra HM là đường trung bình của tam giác BCI.
Do đó HM // BI.
Mà HM ⊥ PH (giả thiết).
Suy ra BI ⊥ PH.
Tam giác BHI có hai đường cao HP, BF cắt nhau tại P.
Suy ra P là trực tâm của tam giác BHI.
Do đó PI ⊥ BH.
Mà BH ⊥ AC (giả thiết).
Vì vậy PI // AC.
Xét ∆HPI và ∆HQC, có:
\(\widehat {PHI} = \widehat {QHC}\) (cặp góc đối đỉnh);
HI = HC (giả thiết);
\(\widehat {HIP} = \widehat {HCQ}\) (do PI // AC, cặp góc so le trong).
Do đó ∆HPI = ∆HQC (g.c.g).
Suy ra HP = HQ.
c) Ta cần chứng minh: cotA.cotB + cotB.cotC + cotC.cotA = 1.
Thật vậy: cotA.cotB + cotB.cotC + cotC.cotA = 1.
\( \Leftrightarrow \frac{1}{{\tan A.\tan B}} + \frac{1}{{\tan B.\tan C}} + \frac{1}{{\tan A.\tan C}} = 1\)
⇔ tanC + tanA + tanB = tanA.tanB.tanC.
Ta có \[\tan \left( {A + B} \right) = \frac{{\tan A + \tan B}}{{1 - \tan A.\tan B}}\].
⇒ tanA + tanB = (1 – tanA.tanB).tan(A + B)
⇒ tanA + tanB + tanC = (1 – tanA.tanB).tan(π – C) + tanC
⇒ tanA.tanB.tanC = –tanC.(1 – tanA.tanB) + tanC
⇒ tanA.tanB.tanC = –tanC + tanA.tanB.tanC + tanC
⇒ tanA.tanB.tanC = tanA.tanB.tanC (luôn đúng).
Vì vậy ta có cotA.cotB + cotB.cotC + cotC.cotA = 1.
Ta có (cotA + cotB + cotC)2
= cot2A + cot2B + cot2C + 2cotA.cotB + 2cotB.cotC + 2cotC.cotA
\( = \frac{1}{2}\left[ {{{\left( {\cot A - \cot B} \right)}^2} + {{\left( {\cot B - \cot C} \right)}^2} + {{\left( {\cot C - \cot A} \right)}^2}} \right]\)
\( + 3\left( {\cot A.\cot B + \cot B.\cot C + \cot C.\cot A} \right) \ge 3\left( {\cot A.\cot B + \cot B.\cot C + \cot C.\cot A} \right)\)
= 3.1 = 3.
Vậy \(\cot A + \cot B + \cot C \ge \sqrt 3 \).
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.
a) Chứng minh AH = DE.
b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.
c) Chứng minh O là trực tâm của tam giác ABQ.
d) Chứng minh SABC = 2SDEQP.
Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.
a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);
b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);
c) \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} \);
d) \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} \).
Từ một điểm A nằm bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.
1) Xác định hình tính của tứ giác AMON.
2) Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O)?
3) Tính diện tích tứ giác AMON.
Tam giác ABC có AB = AC, tia phân giác của \(\widehat A\) cắt BC tại D.
a) Chứng minh rằng AD vuông góc với BC.
b) Lấy điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho BE = CF. Chứng minh rằng DA là tia phân giác của \(\widehat {EDF}\).
Cho tam giác ABC có 3 góc nhọn, AB < AC, đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh .
b) EF cắt CB tại M. Chứng minh MB.MC = ME.MF.
c) Biết SABC = 24, BD = 3 và CD = 5. Tính SBHC.
Cho đường tròn (O; R), đường kính MN. Qua M và N vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở A và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với AP và cắt đường thẳng (d’) ở B.
a) Chứng minh OA = OP.
b) Hạ OH vuông góc với AB. Chứng minh OH = R và AB là tiếp tuyến của đường tròn (O).
c) Chứng minh AM.BN = R2.
d) Tìm vị trí của điểm A để diện tích tứ giác ABNM nhỏ nhất.
Cho tam giác ABC có AB = AC. Tia phân giác \(\widehat A\) cắt BC tại D.
a) Chứng minh DB = DC.
b) Chứng minh AD vuông góc BC.
Cho tứ diện ABCD với \(AC = \frac{3}{2}AD,\,\,\widehat {CAB} = \widehat {DAB} = 60^\circ ,\,\,CD = AD\). Gọi φ là góc giữa hai đường thẳng AB và CD. Chọn khẳng định đúng về góc φ.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC.
a) Chứng minh \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).
b) Xác định điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0\).
Cho tam giác ABC vuông tại A có AB = AC. Qua A vẽ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:
a) ∆BAM = ∆ACN;
b) MN = BM + CN.
Cho biểu thức \(P = \frac{{{x^2} + x}}{{{x^2} - 2x + 1}}:\left( {\frac{{x + 1}}{x} - \frac{1}{{1 - x}} + \frac{{2 - {x^2}}}{{{x^2} - x}}} \right)\).
a) Rút gọn P.
b) Tìm x để P < 1.
c) Tìm giá trị nhỏ nhất của P khi x > 2.
