Cho tam giác cân ABC có CA = CB và góc ABC nhọn. Các đường cao CD, BE, AF cắt nhau ở H.
a) Chứng minh 4 điểm C, F, H, E nằm trên đường tròn (O). Xác định tâm O của đường tròn.
b) Chứng minh (O) tiếp xúc với đường tròn ngoại tiếp tam giác ABC.
c) Chứng minh DF là tiếp tuyến của đường tròn (O).
d) Chứng minh FB là phân giác của góc DFE.
Giải bởi Vietjack
Lời giải
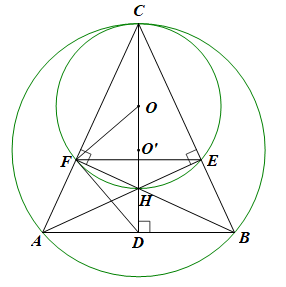
a) Ta có: \(AE \bot BC,BF \bot AC\) nên \[\widehat {CFH} = \widehat {CEH} = 90^\circ \].
Do đó F, E cùng nằm trên đường tròn đường kính CH.
Suy ra 4 điểm C, F, H, E cùng nằm trên đường tròn (O) đường kính CH với O là trung điểm của CH.
b) Gọi (O’) là đường tròn ngoại tiếp tam giác ABC.
Do tam giác ABC có CA = CB nên tam giác ABC cân tại C
Do đó tâm O’ của đường tròn ngoại tiếp tam giác nằm trên đường cao CD.
Suy ra 3 điểm C, O, O’ thẳng hàng và OO’ = O’C – OC.
Lại có C cùng nằm trên đường tròn (O) và (O’)
Vậy (O) tiếp xúc với (O’) với (O’) là đường tròn ngoại tiếp tam giác ABC.
c) Chứng minh tương tự câu a ta cũng có tứ giác AFHD là tứ giác nội tiếp
Suy ra \(\widehat {HFD} = \widehat {HAD}\) (hai góc nội tiếp cùng chắn cung HD).
Lại có \(\widehat {HAD} = \widehat {ECH}\) (do cùng phụ với \(\widehat {AHD} = \widehat {CHE}\))
\(\widehat {ECH} = \widehat {FCH}\) (do tam giác ABC cân tại C nên CH là đường phân giác)
\(\widehat {FCH} = \widehat {FCO} = \widehat {CFO}\) (do tam giác OCF có OC = OF nên là tam giác cân tại O)
Do đó \(\widehat {HFD} = \widehat {CFO}\).
Mặt khác \(\widehat {CFO} + \widehat {OFH} = 90^\circ \) nên \(\widehat {HFD} + \widehat {{\rm{OF}}H} = 90^\circ \)
Hay \(\widehat {DFO} = 90^\circ \)
Mà F nằm trên (O) nên DF là tiếp tuyến của (O).
d) Do DF là tiếp tuyến của (O) nên \(\widehat {DFH} = \widehat {FCH}\) (tính chất góc tạo bởi tia tiếp tuyến và dây cung với góc nội tiếp đường tròn cùng chắn cung đó)
Ta cũng có \(\widehat {EFH} = \widehat {ECH}\) (hai góc nội tiếp cùng chắn cung EH)
Mà \(\widehat {FCH} = \widehat {ECH}\) (do CH là phân giác của góc ACB)
Suy ra \(\widehat {EFH} = \widehat {DFH}\)
Do đó FB là phân giác của \(\widehat {DFE}\).
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh và SAEF = cos2A.SABC.
b) Gọi M là trung điểm của BC. Đường thẳng vuông góc với HM tại H cắt AB, AC lần lượt tại P và Q. Chứng minh PH = QH.
c) Chứng minh \(\cot A + \cot B + \cot C \ge \sqrt 3 \).
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.
a) Chứng minh AH = DE.
b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.
c) Chứng minh O là trực tâm của tam giác ABQ.
d) Chứng minh SABC = 2SDEQP.
Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.
a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);
b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);
c) \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} \);
d) \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} \).
Từ một điểm A nằm bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.
1) Xác định hình tính của tứ giác AMON.
2) Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O)?
3) Tính diện tích tứ giác AMON.
Tam giác ABC có AB = AC, tia phân giác của \(\widehat A\) cắt BC tại D.
a) Chứng minh rằng AD vuông góc với BC.
b) Lấy điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho BE = CF. Chứng minh rằng DA là tia phân giác của \(\widehat {EDF}\).
Cho tam giác ABC có 3 góc nhọn, AB < AC, đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh .
b) EF cắt CB tại M. Chứng minh MB.MC = ME.MF.
c) Biết SABC = 24, BD = 3 và CD = 5. Tính SBHC.
Cho đường tròn (O; R), đường kính MN. Qua M và N vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở A và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với AP và cắt đường thẳng (d’) ở B.
a) Chứng minh OA = OP.
b) Hạ OH vuông góc với AB. Chứng minh OH = R và AB là tiếp tuyến của đường tròn (O).
c) Chứng minh AM.BN = R2.
d) Tìm vị trí của điểm A để diện tích tứ giác ABNM nhỏ nhất.
Cho tam giác ABC có AB = AC. Tia phân giác \(\widehat A\) cắt BC tại D.
a) Chứng minh DB = DC.
b) Chứng minh AD vuông góc BC.
Cho tứ diện ABCD với \(AC = \frac{3}{2}AD,\,\,\widehat {CAB} = \widehat {DAB} = 60^\circ ,\,\,CD = AD\). Gọi φ là góc giữa hai đường thẳng AB và CD. Chọn khẳng định đúng về góc φ.
Cho tam giác ABC vuông tại A có AB = AC. Qua A vẽ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:
a) ∆BAM = ∆ACN;
b) MN = BM + CN.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC.
a) Chứng minh \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).
b) Xác định điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0\).
