Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và SA vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SBD).
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
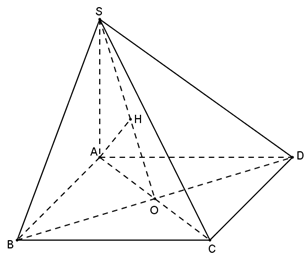
Gọi O là giao điểm của AC và BD.
Gọi H là hình chiếu của lên SO.
Ta có và nên .
Lại có và nên .
Trong tam giác ABC có .
Trong tam giác SAO có .
Vậy .Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp đã cho bằng:
Cho hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên với đáy một góc 45o. Tính cosin của góc giữa mặt bên và đáy của hình chóp đã cho.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu . Tìm tất cả các giá trị thực dương của tham số m để mặt phẳng x - 2y + 2z + m = 0 tiếp xúc với mặt cầu (S)
Hình chiếu vuông góc của điểm M(1;-2;3) lên mặt phẳng (Oyz) có toạ độ là: