Giải bởi Vietjack
Lời giải
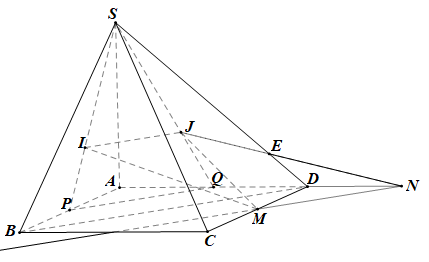
Gọi P, Q lần lượt là trung điểm của AB, AD.
Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.
Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên \(\frac{{SI}}{{SP}} = \frac{2}{3} = \frac{{SJ}}{{SQ}}\).
Do đó IJ // PQ, suy ra IJ // BD
Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)
Þ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.
Đường thẳng này cắt AD tại N.
Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)
Trong mp(SAN), JN cắt SD tại E.
Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)
Khi đó E là giao điểm của SD và (IJM).
Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H.
a) Chứng minh tứ giác AEHF nội tiếp.
b) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF. Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu \(\widehat {BAC} = 60^\circ \), AH = 4 cm.
c) AH giao BC tại D. Chứng minh FH là tia phân giác của \(\widehat {DFE}\).
d) Chứng minh 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại một điểm.
Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại D và E.
a) Chứng minh CD vuông góc với AB, BE vuông góc với AC.
b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của cạnh BC.
a) Chứng minh rằng ∆ABD = ∆ACD và AD là tia phân giác của \(\widehat {BAC}\).
b) Vẽ DM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho AN = AM. Chứng minh ∆ADM = ∆ADN và DN vuông góc AC.
c) Gọi K là trung điểm của đoạn thẳng CN. Trên tia đối của tia KD lấy điểm E sao cho KE = KD. Chứng minh M, E, N thẳng hàng.
Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh:
a) ∆ADB = ∆ADC.
b) AD là tia phân giác của \(\widehat {BAC}\) và \(\widehat B = \widehat C\).
c) AD vuông góc với BC.
a) Cho biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\] với x ≥ 0. Tính giá trị của A khi x = 16.
b) Cho biểu thức \(B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\) với x ≥ 0; x ≠ 1. Rút gọn B.
c) Tìm các số hữu tỉ x để P = A.B có giá trị nguyên.
Cho tam giác ABC. Hãy tìm các điểm M thỏa các điều kiện:
a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \).
b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB} \).
c) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \).
d) \(\left| {\overrightarrow {MA} - \overrightarrow {CA} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AB} } \right|\).
Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:
a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \).
b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB} \).
c) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).
