Giải bởi Vietjack
Lời giải:
Xét n > 9 \( \Rightarrow \) A = 29 + 213 + 2n = 29(1 + 24 + 22n-9).
Thấy (1 + 24 + 22n-9) là số lẻ nên A chia hết cho 29 nhưng không chia cho 210 nên A không là số chính phương
• Xét n = 9, ta có:
A = 29 + 213 + 29 = 29(1 + 24 + 1) = 9. 210 = 962 là số chính phương.
• Xét n < 9, ta có:
A = 29 + 213 + 2n = 2n(29-n + 213-n + 1)
Do 29-n + 213-n + 1 là số lẻ và A là số chính phương nên 2n là số chính phương nên n là số chẵn, n ∈ ℕ* suy ra n ∈ {2; 4; 6; 8}
Khi đó A chính phương, 2n chính phương suy ra B = 29-n + 213-n + 1 là số chính phương Nhận xét số chính phương lẻ chỉ có thể tận cùng là 1; 5; 9.
• Với n = 2 \( \Rightarrow \) B = 27 + 211 + 1 = 2177 (loại)
• Với n = 4 \( \Rightarrow \) B = 25 + 29 + 1 = 545, thấy B chia hết cho 5 nhưng không chia hết cho 25 nên B không là số chính phương.
• Với n = 6 \( \Rightarrow \) B = 23 + 27 + 1 = 137 (loại)
• Với n = 8 \( \Rightarrow \) B =2 + 25 + 1 = 35 (loại)
Vậy n = 9
Một thửa ruộng hình chữ nhật có chiều dài là 100 m, chiều rộng bằng \(\frac{4}{5}\) chiều dài. Tính diện tích thửa ruộng đó.
Biết rằng cứ 1 m2 người nông dân thu hoạch được 6 kg thóc. Hỏi trên thửa ruộng đó người ta thu hoạch được bao nhiêu tạ thóc.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ:
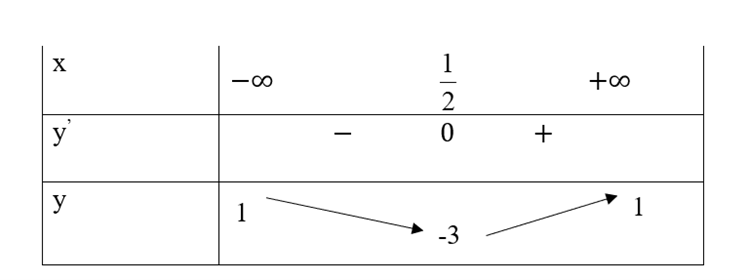
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số: \[y = \frac{1}{{2f(x) - 1}}\] là bao nhiêu?
Một thửa ruộng hình chữ nhật có chiều dài 100 m, chiều rộng bằng \[\frac{2}{3}\]chiều dài.
a) Tính diện tích của thửa ruộng hình chữ nhật đó?
b) Cứ 100 m thu hoạch được 50 kg thóc. Hỏi trên thử ruộng đó thu hoạch được bao nhiêu tạ thóc?
a) Mẹ mua 5 kg đường phải trả 60 000 đồng. Hỏi mua 8 kg đường như thế phải trả bao nhiêu tiền?
b)Nếu giá mỗi ki-lô-gam đường giảm đi 2 000 đồng thì với 60 000 đồng có thể mua được bao nhiêu ki-lô-gam đường như thế?
Trên đưởng thẳng xy lấy 4 điểm A, B, C, D theo thứ tự ấy, sao cho AB = CD
Chứng minh AC = BD
