Phân tích mỗi đa thức sau thành nhân tử:
a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy);
b) 8x3yz + 12x2yz + 6xyz + yz.
Giải bởi Vietjack
Lời giải
a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy)
= x3(13xy ‒ 5) + y3(13xy ‒ 5)
= (13xy ‒ 5)(x3 + y3)
= (13xy ‒ 5)(x + y)(x2 ‒ xy + y2).
b) 8x3yz + 12x2yz + 6xyz + yz
= yz(8x3 + 12x2 + 6x + 1)
= yz[(2x)3 + 3.(2x)2.1 + 3.2x.12 + 13)]
= yx(2x + 1)3.
Tính giá trị của mỗi biểu thức sau:
a) \(A = {x^2} + xy + \frac{{{y^2}}}{4}\) biết \(x + \frac{y}{2} = 100\).
b) B = 25x2z ‒ 10xyz + y2z biết 5x ‒ y = ‒20 và z = ‒5.
c) C = x3yz + 3x2y2z + 3xy3z + y4z biết x + y = ‒0,5 và yz = 8.
Phân tích mỗi đa thức sau thành nhân tử:
a) \(25{x^2} - \frac{1}{4}\);
b) 36x2 + 12xy + y2;
c) \(\frac{{{x^3}}}{2} + 4\);
d) 27y3 + 27y2 + 9y + 1.
Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0 và hình vuông MNPQ có cạnh MN = y (dm) với y > 0 (Hình 4).
=
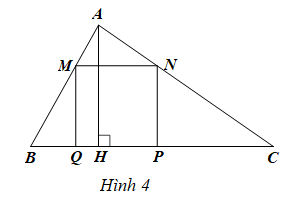
a) Viết công thức tính tổng diện tích của các tam giác AMN, BMQ, CNP dưới dạng tích.
b) Tính tổng diện tích của các tam giác AMN, BMQ, CNP, biết x ‒ y = 2 và x + y = 10.
