Giải bởi Vietjack
Lời giải
Ta có cos2x + 3sinx – 2 = 0.
⇔ –2sin2x + 3sinx – 1 = 0.
\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x = \frac{1}{2}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\).
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{\pi }{2} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{\pi }{2} < k2\pi < \frac{{39\pi }}{2}\).
\( \Leftrightarrow - \frac{1}{4} < k < \frac{{39}}{4}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (1)
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{\pi }{6} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{\pi }{6} < k2\pi < \frac{{119\pi }}{6}\).
\( \Leftrightarrow - \frac{1}{{12}} < k < \frac{{119}}{{12}}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (2)
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{{5\pi }}{6} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{{5\pi }}{6} < k2\pi < \frac{{115\pi }}{6}\).
\( \Leftrightarrow - \frac{5}{{12}} < k < \frac{{115}}{{12}}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (3)
Từ (1), (2), (3), ta thu được số nghiệm của phương trình đã cho trên khoảng (0; 20π) là 30.
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC.
a) Chứng minh rằng BE = CD.
b) Chứng minh BE // CD.
c) Gọi M là trung điểm của BE và N là trung điểm của CD. Chứng minh AM = AN.
a) Viết phương trình đường thẳng biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và cắt trục hoành tại điểm có hoành độ bằng –3.
b) Viết phương trình đường thẳng (d) biết (d) có hệ số góc là –2 và đi qua điểm A(–1; 5).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
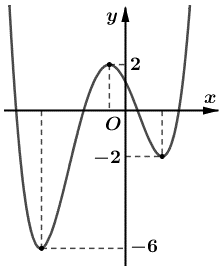
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0).
a) Tìm m để đồ thị hàm số (1) đi qua điểm M(1; 3).
b) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 4. Vẽ đồ thị hàm số với m tìm được.
