Giải bởi Vietjack
Lời giải
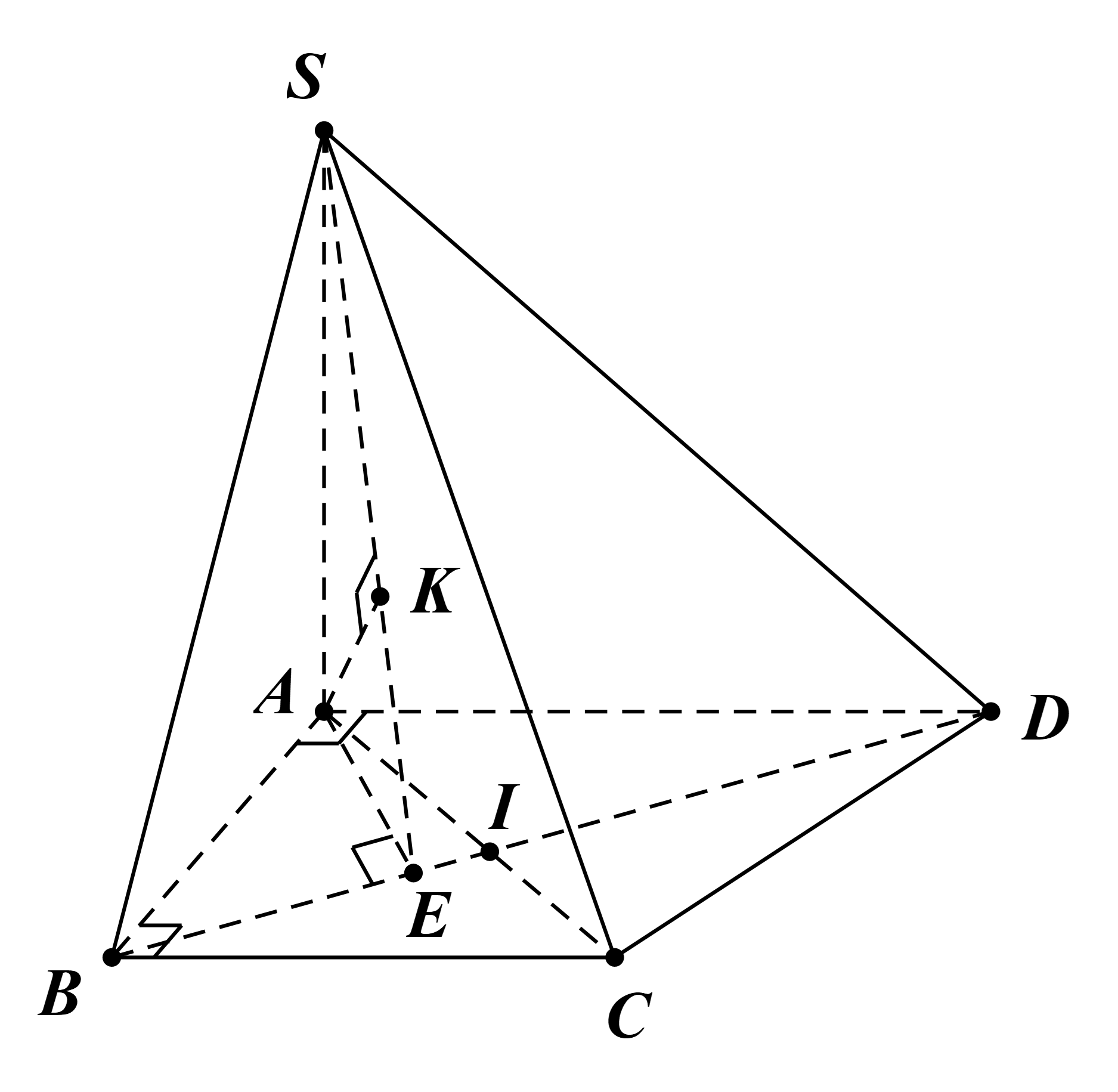
Trong (ABCD): kẻ AE ⊥ BD.
Trong (SAE): kẻ AK ⊥ SE.
Ta có BD ⊥ AE và BD ⊥ SA.
Suy ra BD ⊥ (SAE).
Do đó BD ⊥ AK.
Mà AK ⊥ SE.
Vì vậy AK ⊥ (SBD).
Khi đó d(A, (SBD)) = AK.
Tam giác ABD vuông tại A có AE là đường cao:
\(AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{a.a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}\).
Tam giác SAE vuông tại A có AK là đường cao:
\(AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \frac{{a\sqrt 2 .\frac{{a\sqrt 6 }}{3}}}{{\sqrt {2{a^2} + \frac{{2{a^2}}}{3}} }} = \frac{{a\sqrt 2 }}{2}\).
Do đó \(d\left( {A,\left( {SBD} \right)} \right) = AK = \frac{{a\sqrt 2 }}{2}\).
Trong (ABCD): gọi I = AC ∩ BD.
Ta có AB = BC = a và \(\widehat {ABC} = 90^\circ \).
Suy ra tam giác ABC vuông cân tại B.
Do đó \(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \) và \(\widehat {BAC} = \widehat {BCA} = 45^\circ \).
Mà \(\widehat {IAD} = \widehat {BAD} - \widehat {BAC} = 45^\circ \).
Suy ra AI là tia phân giác của \(\widehat {BAD}\).
Áp dụng tính chất đường phân giác, ta có: \(\frac{{IB}}{{ID}} = \frac{{AB}}{{AD}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\).
Do đó \(ID = \sqrt 2 IB\).
Ta có \(IB + ID = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 3 \).
\( \Rightarrow IB + \sqrt 2 IB = a\sqrt 3 \).
\( \Rightarrow IB = \frac{{a\sqrt 3 }}{{1 + \sqrt 2 }} = a\left( {\sqrt 6 - \sqrt 3 } \right)\).
Ta có \(I{B^2} = A{B^2} + A{I^2} - 2AB.AI.\cos \widehat {BAI}\).
\[ \Rightarrow A{I^2} - a\sqrt 2 .AI + \left( {6\sqrt 2 - 8} \right){a^2} = 0\].
\( \Rightarrow \left[ \begin{array}{l}AI = a\left( {2\sqrt 2 - 2} \right)\\AI = a\left( {2 - \sqrt 2 } \right)\end{array} \right.\)
Vì AI > IB nên ta nhận \(AI = a\left( {2\sqrt 2 - 2} \right)\).
Với \(AI = a\left( {2\sqrt 2 - 2} \right)\), ta có \(IC = AC - AI = a\left( {2 - \sqrt 2 } \right)\).
Khi đó \(d\left( {C,\left( {SBD} \right)} \right) = \frac{{IC}}{{IA}}.d\left( {A,\left( {SBD} \right)} \right) = \frac{{a\left( {2 - \sqrt 2 } \right)}}{{a\left( {2\sqrt 2 - 2} \right)}}.\frac{{a\sqrt 2 }}{2} = \frac{a}{2}\).
Vậy khoảng cách h từ C đến mặt phẳng (SBD) bằng \(\frac{a}{2}\).
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC.
a) Chứng minh rằng BE = CD.
b) Chứng minh BE // CD.
c) Gọi M là trung điểm của BE và N là trung điểm của CD. Chứng minh AM = AN.
a) Viết phương trình đường thẳng biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và cắt trục hoành tại điểm có hoành độ bằng –3.
b) Viết phương trình đường thẳng (d) biết (d) có hệ số góc là –2 và đi qua điểm A(–1; 5).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
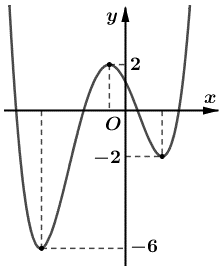
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0).
a) Tìm m để đồ thị hàm số (1) đi qua điểm M(1; 3).
b) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 4. Vẽ đồ thị hàm số với m tìm được.
