Đáp án đúng là: C

Điều kiện x ∈ ℝ

Ta có: \({2^{{{\left( {x - 1} \right)}^2}}}.{\log _2}\left( {{x^2} - 2{\rm{x}} + 3} \right) = {4^{\left| {x - m} \right|}}{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\)

\( \Leftrightarrow {2^{{{\left( {x - 1} \right)}^2}}}.{\log _2}\left[ {{{\left( {x - 1} \right)}^2} + 2} \right] = {2^{2\left| {x - m} \right|}}{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\)                      (1)

Xét hàm số \(y = {2^t}.{\log _2}\left( {t + 2} \right)\) với t ≥ 0

Hàm số \(y = {2^t}.{\log _2}\left( {t + 2} \right)\) xác định và liên tục trên [0; +∞)

Ta có: \(y' = {2^t}.{\log _2}\left( {t + 2} \right).\ln 2 + \frac{{{2^t}}}{{\left( {t + 2} \right)\ln 2}} > 0\)

Suy ra hàm số \(y = {2^t}.{\log _2}\left( {t + 2} \right)\) đồng biến trên [0; +∞)

Ta có: \(\left( 1 \right) \Leftrightarrow f\left( {{{\left( {x - 1} \right)}^2}} \right) = f\left( {2\left| {x - m} \right|} \right)\)

\( \Leftrightarrow {\left( {x - 1} \right)^2} = 2\left| {x - m} \right|\)

\( \Leftrightarrow \left[ \begin{array}{l}{\left( {x - 1} \right)^2} = 2\left( {x - m} \right)\\{\left( {x - 1} \right)^2} = 2\left( {m - x} \right)\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2{\rm{x + }}1 = 2x - 2m\\{x^2} - 2{\rm{x}} + 1 = 2m - 2{\rm{x}}\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l} - {x^2} + 4{\rm{x}} - 1 = 2m\\{x^2} + 1 = 2m\end{array} \right.\left( * \right)\)

Xét phương trình 2m = – x² + 4x – 1

Ta có bảng biến thiên của hàm số g(x) = – x² + 4x – 1

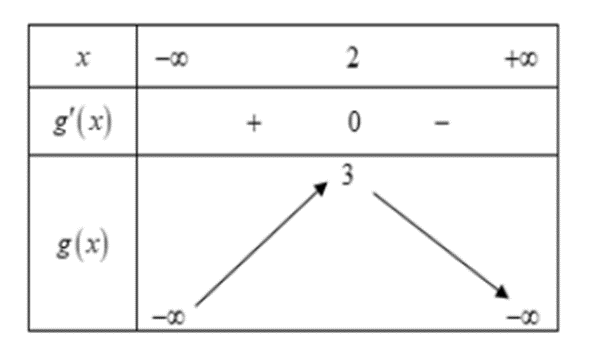
Phương trình 2m = – x² + 4x – 1 có 2 nghiệm phân biệt khi 2m < 3 hay \(m < \frac{3}{2}\)

Phương trình 2m = – x² + 4x – 1 có 1 nghiệm phân biệt khi 2m = 3 hay \(m = \frac{3}{2}\)

Phương trình 2m = – x² + 4x – 1 vô nghiệm phân biệt khi 2m > 3 hay \(m > \frac{3}{2}\)

Xét phương trình 2m = x² + 1

Ta có bảng biến thiên của hàm số h(x) = x² + 1

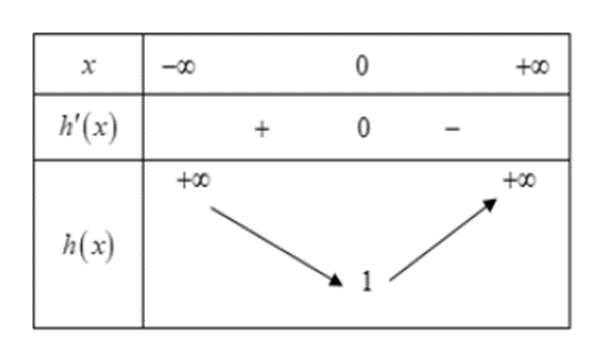
Phương trình 2m = x² + 1 có 2 nghiệm phân biệt khi 2m > 1 hay \(m > \frac{1}{2}\)

Phương trình 2m = x² + 1 có 1 nghiệm phân biệt khi 2m = 1 hay \(m = \frac{1}{2}\)

Phương trình 2m = x² + 1 vô nghiệm phân biệt khi 2m < 1 hay \(m < \frac{1}{2}\)

+) Khi \(m = \frac{3}{2}\) phương trình 2m = – x² + 4x – 1 có 1 nghiệm x = 2, phương trình 2m = x² + 1 có 2 nghiệm \[{\rm{x}} = \pm \sqrt 2 \]

Suy ra (*) có 3 nghiệm phân biệt nên loại \(m = \frac{3}{2}\)

+) Khi \(m = \frac{1}{2}\) phương trình 2m = – x² + 4x – 1 có 2 nghiệm \[{\rm{x}} = 2 \pm \sqrt 2 \], phương trình 2m = x² + 1 có 1 nghiệm x = 0

Suy ra (*) có 3 nghiệm phân biệt nên loại \(m = \frac{1}{2}\)

+) Xét phương trình – x² + 4x – 1 = x² + 1

⇔ 2x² – 4x + 2 = 0

⇔ 2(x – 1)² = 0

⇔ x = 1

Suy ra không tồn tại m để (*) có 2 nghiệm phân biệt

Để phương trình \({2^{{{\left( {x - 1} \right)}^2}}}.{\log _2}\left( {{x^2} - 2{\rm{x}} + 3} \right) = {4^{\left| {x - m} \right|}}{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\) có đúng 2 nghiệm phân biệt

\( \Leftrightarrow \left[ \begin{array}{l} - {x^2} + 4{\rm{x}} - 1 = 2m\\{x^2} + 1 = 2m\end{array} \right.\left( * \right)\) có đúng hai nghiệm phân biệt

TH1: Phương trình 2m = – x² + 4x – 1 có 2 nghiệm phân biệt và phương trình 2m = x² + 1 vô nghiệm

\( \Leftrightarrow \left\{ \begin{array}{l}m < \frac{3}{2}\\m < \frac{1}{2}\end{array} \right. \Leftrightarrow m < \frac{1}{2}\)

TH2: Phương trình 2m = – x² + 4x – 1 vô nghiệm và phương trình 2m = x² + 1 có 2 nghiệm phân biệt

\( \Leftrightarrow \left\{ \begin{array}{l}m > \frac{3}{2}\\m > \frac{1}{2}\end{array} \right. \Leftrightarrow m > \frac{3}{2}\)

TH3: Phương trình 2m = – x² + 4x – 1 có nghiệm x = 2 và phương trình 2m = x² + 1 có nghiệm x = 0

\( \Leftrightarrow \left\{ \begin{array}{l}m = \frac{3}{2}\\m = \frac{1}{2}\end{array} \right. \Leftrightarrow m \in \emptyset \)

Mà m ∈ [– 2019; 2019]

Nên \(m \in \left[ { - 2019;\left. {\frac{1}{2}} \right) \cup \left( {\frac{3}{2};\left. {2019} \right]} \right.} \right.\)

Vì m nguyên nên ta có 4038 giá trị của m

Vậy ta chọn đáp án C.