Cho hình thang cân ABCD, có đáy nhỏ và đường cao cùng bẳng 2a và \(\widehat {ABC} = 45^\circ \). Tính \(\left| {\overrightarrow {CB} - \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} } \right|\).
A. \[a\sqrt 3 \]
B. \(2{\rm{a}}\sqrt 5 \)
C. \[{\rm{a}}\sqrt 5 \]
D. \[{\rm{a}}\sqrt 2 \].
Giải bởi Vietjack
Đáp án đúng là: B
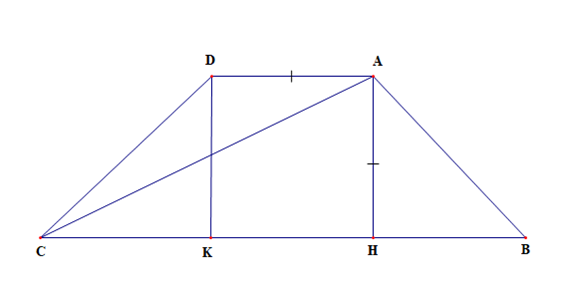
Gọi H, K là chân đường cao hạ từ A, D xuống BC
Khi đó tam giác ABH vuông tại H
Mà \(\widehat {ABC} = 45^\circ \)
Suy ra tam giác ABH vuông cân tại H
Do đó AH = BH = 2a
Vì hình thang ABCD cân
Nên AB = CD, \(\widehat {ABC} = \widehat {DCB}\), BD = AC
Xét tam giác ABH và tam giác DCK có
\(\widehat {AHB} = \widehat {DKC}\left( { = 90^\circ } \right)\)
AB = CD
\(\widehat {ABC} = \widehat {DCB}\)
Suy ra ∆ABH = ∆DCK (cạnh huyền – góc nhọn)
Do đó CK = BH = 2a
Ta có CH = AD + CK = 2a + 2a = 4a
Xét tam giac AHC vuông tại H có
AC2 = AH2 + CH2
Suy ra \[{\rm{AC = }}\sqrt {{{\left( {2{\rm{a}}} \right)}^2} + {{\left( {4{\rm{a}}} \right)}^2}} = 2{\rm{a}}\sqrt 5 \]
Ta có:
\(\left| {\overrightarrow {CB} - \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DA} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = AC = 2{\rm{a}}\sqrt 5 \)
Vậy ta chọn đáp án B.
Với a, b là các số thực dương tùy ý thỏa mãn log3a – 2log9b = 2, mệnh đề nào dưới đây đúng?
Xếp 6 người A, B, C, D, E, F vào một ghế dài. Hỏi có bao nhiêu cách sắp xếp sao cho A và F không ngồi cạnh nhau.
Tìm số nguyên a, b biết \(\frac{a}{7} - \frac{1}{2} = \frac{1}{{b + 3}}\).
Cho x, y, z là các số thực dương và thỏa mãn điều kiện x + y + z = xyz. Tìm giá trị lớn nhất của: \(P = \frac{1}{{\sqrt {1 + {x^2}} }} + \frac{1}{{\sqrt {1 + {y^2}} }} + \frac{1}{{\sqrt {1 + {z^2}} }}.\)
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \(\log _2^2x + 4{\log _2}x - m = 0\) có nghiệm thuộc khoảng (0; 1).
Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) có điểm đầu và điểm cuối là đỉnh của lục giác.
Tìm tập hợp các giá trị của tham số thực m để phương trình 6x + (3 – m) . 2x – m = 0 có nghiệm thuộc khoảng (0; 1).
Cho phương trình \({2^{{{\left( {x - 1} \right)}^2}}}.{\log _2}\left( {{x^2} - 2{\rm{x}} + 3} \right) = {4^{\left| {x - m} \right|}}{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\) với m là tham số thực. Có bao nhiêu giá trị nguyên của m trên đoạn [–2019; 2019] để phương trình có đúng 2 nghiệm phân biệt.
Gọi S là tập hợp các giá trị nguyên dương của m để hàm số y = x3 – 3(2m + 1)x2 + (12m + 5)x + 2 đồng biến trên khoảng (2; +∞). Số phần tử của S bằng
Giải phương trình: \(\left( {x + 1} \right)\left( {x + 4} \right) - 3\sqrt {{x^2} + 5{\rm{x}} + 2} = 6\).
Chứng minh đẳng thức sau: (x + y + z)3 = x3 + y3 + z3 + 3(x + y)(y + z)(z + x).
