Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Điểm C là trọng tâm của tam giác nào?
A. ΔABD;
B. ΔADE;
C. ΔABE;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B
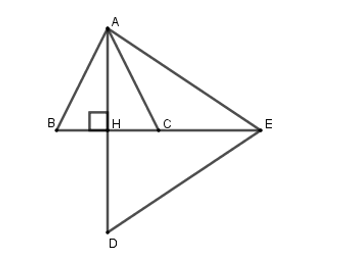
Xét ∆AHB (vuông tại H) và AHC (vuông tại H) có:
AB = AC (do ΔABC cân tại A);
AH là cạnh chung
Do đó: ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)
Suy ra HB = HC (hai cạnh tương ứng)
Ta có CE = CB = HB + HC = 2CH
Xét ΔADE có EH là đường trung tuyến mà CE = 2CH nên C là trọng tâm của ΔADE.
Cho ΔABC cân tại A có hai đường trung tuyến BM, CN cắt nhau tại G. Tam giác GBC là tam giác
Cho tam giác ABC cân tại A. Đường phân giác của góc A cắt đường trung tuyến BD tại K. Gọi I là trung điểm của AB. Khẳng định nào sau đây là sai?
Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD = CE. Khi đó tam giác ABC là tam giác
Cho ΔABC vuông tại A, trung tuyến AM. Khẳng định nào sau đây là đúng?
Cho ΔABC có hai đường trung tuyến BN, CP vuông góc với nhau tại G. Biết độ dài BC = 5cm. Độ dài AG là:
Cho tam giác ABC, AM là đường trung tuyến. Biết AM = MB = MC. Cho biết tam giác ABC là tam giác gì?
Cho G là trọng tâm của tam giác đều ABC. Khẳng định nào sau đây là đúng?