Họ tất cả các nguyên hàm của hàm số là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần xuất hiện mặt ngửa là
Cho hình chóp tam giác đều SABC có AB =a, khoảng cách giữa hai đường thẳng SA và BC bằng (tham khảo hình vẽ).
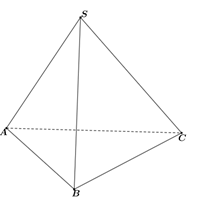
Thể tích khối chóp SABC bằng
Xét các số phức z thỏa mãn . Biết giá trị lớn nhất của biểu thức có dạng . Giá trị của biểu thức a -b bằng
Trong mặt phẳng tọa độ Oxy, biết tập hợp điểm biểu diễn của số phức z thỏa mãn là đường thẳng d. Phương trình đường thẳng d là
Cho hàm số f(x), g(x) liên tục trên R. Trong các mệnh đề sau, mệnh đề nào sau sai?
Trong không gian Oxyz, hình chiếu của điểm A(1;2-1) trên mặt phẳng (Oxy) là điểm nào dưới đây?
Cho hình hộp ABCD.A'B'C'D' có ( tham khảo hình vẽ). Góc giữa hai đường thẳng AB và A'C' bằng
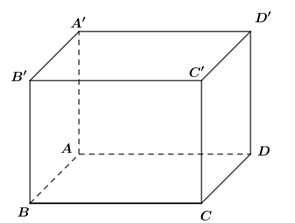
Đặt . Có bao nhiêu giá trị nguyên của a thuộc khoảng (0;2023) để ?
Cho hàm số y=f(x) có đạo hàm , . Số giá trị nguyên của tham số m để hàm số có 8 điểm cực trị là
Cho x,y là các số thực dương thỏa mãn . Tính giá trị lớn nhất của biểu thức .
Cho hàm số f(x) có đạo hàm liên tục trên [1;2], f(1)=1 và f(2)=2. Tính .
Trên tập số phức, xét phương trình (m là tham số thực). Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn .
Trong không gian Oxyz, gọi a là góc giữa hai mặt phẳng và . Tính .