Cho số phức z thỏa mãn . Giá trị nhỏ nhất của biểu thức P = |z – 2 – i| + |z – 3 – 2i| bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
.
Khi đó điểm M biểu diễn số phức z trên mặt phẳng phức là gốc tọa độ O (0;0) hoặc thuộc đường thẳng d: x = 0 với d là đường trung trực của đoạn thẳng AB với A (0;1), B (0;-1).
TH1: , .
TH2: , P = MC + MD với C (2;1) và D (3;2).
Do C (2;1) và D (3;2) khác phía so với d: x = 0 nên gọi C' (2;-1) là điểm đối xứng của C qua d: x = 0. Khi đó .
Vậy giá trị nhỏ nhất của là .
Cho hàm số f(x) liên tục trên R. Gọi F(x), G(x) là hai nguyên hàm của f(x) trên R thỏa mãn F(8) + G(8) = 4. Cho biết ![]() , giá trị của F912) + G(12) bằng
, giá trị của F912) + G(12) bằng
Trong không gian Oxyz, gọi M là giao điểm của đường thẳng và mặt phẳng (P) : x + y + z – 3 = 0. Điểm M có tọa độ là
Trong không gian Oxyz, cho mặt phẳng (Q): x + 2y – z + 3 = 0. Vectơ nào sau đây vuông góc với vectơ pháp tuyến của mặt phẳng (Q)?
Trong mặt phẳng tọa độ Oxyz, tập hợp các điểm biểu diễn cho số phức z thỏa mãn là đường thẳng
Trong không gian Oxyz, cho điểm A (4;0;0), B (1;2;3). Gọi M là điểm di động thỏa mãn và . Gọi p,q lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của BM. Giá trị bằng
Cho bất phương trình có tập nghiệm là S (a;b). Khi đó b - a gần bằng giá trị nào sau đây?
Cho hàm số y = f(x) có đồ thị là đường cong như hình vẽ.
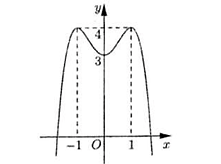
Tọa độ giao điểm của đồ thị đã cho và trục tung là
Trong không gian Oxyz cho điểm A (1;3;4). Điểm đối xứng của A qua trục Ox có tọa độ là
Cho hình lăng trụ đều ABC.A’B’C’ (tham khảo hình vẽ) có AA’ = 2a, AB = a.
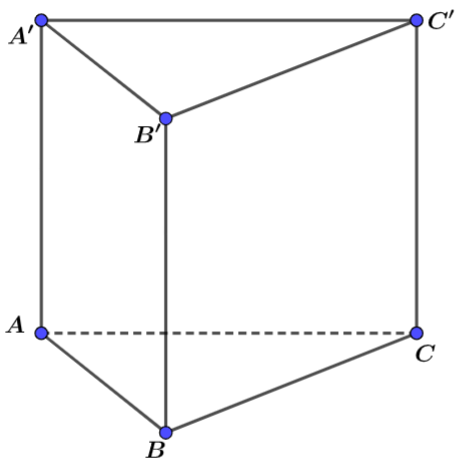
Khoảng cách từ C’ tới mặt phẳng (B’AC) bằng
Cho đường thẳng d cắt mặt cầu S(O;R) tại hai điểm phân biệt. Gọi H là hình chiếu vuông góc của O lên đường thẳng d. Khẳng định nào sau đây là đúng?
Trong không gian Oxyz, cho A (0;1;0), góc giữa đường thẳng OA và mặt phẳng (Oxz) bằng
Một hộp chứa 10 quả bóng gồm 4 quả màu đỏ kích thước khác nhau và 6 quả màu xanh kích thước khác nhau. Lấy ngẫu nhiên đồng thời 3 quả từ hộp. Xác suất để 3 quả lấy được đều màu đỏ bằng