Phần ảo của số phức z = 3 – 4i bằng

Trong không gian Oxyz, cho hai vec tơ $\overrightarrow{u}=\left(1;1;0\right)$  và $\overrightarrow{v}=\left(2;0;-1\right)$ . Tính độ dài $\left|\overrightarrow{u}+2\overrightarrow{v}\right|$ .

Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn là

Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới.

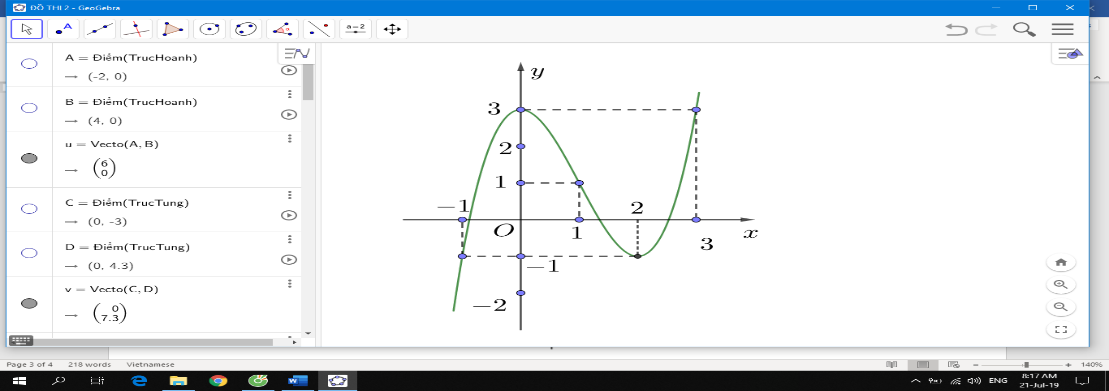
Số nghiệm thực của phương trình $\left|f\left(x^4-2x^2\right)\right|=2$  là

Trên tập hợp số phức, xét phương trình $z^2-6z+m=0\left(m\right.$  là tham số thực). Gọi $m_0$  là một giá trị nguyên của m  để phương trình đó có hai nghiệm phân biệt $z_1,z_2$  thỏa mãn $z_1.\overline{z_1}=z_2.\overline{z_2}$ . Trong khoảng (0;20) có bao nhiêu giá trị nguyên $m_0$ ?

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong ở hình bên dưới.

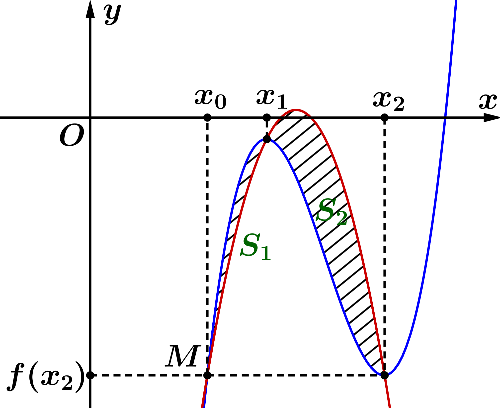
Gọi $x_1,x_2$  lần lượt là hai điểm cực trị thỏa mãn $x_2=x_1+2$  và $f\left(x_1\right)-3f\left(x_2\right)=0$.  và đồ thị luôn đi qua $M\left(x_0;f\left(x_0\right)\right)$, trong đó $x_0=x_1-1; g\left(x\right)$  là hàm số bậc hai có đồ thị qua 2 điểm cực trị của đồ thị hàm số y = f(x) và điểm M. Tính tỉ số $\frac{S_1}{S_2}$($S_1$ và $S_2$  lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm $f\left(x\right),g\left(x\right)$  như hình vẽ).

Trong không gian Oxyz, cho hai điểm A (2;1;3), B (6;5;5). Xét khối nón (N) ngoại tiếp mặt cầu đường kính AB có B là tâm đường tròn đáy khối nón. Gọi S là đỉnh của khối nón (N). Khi thể tích khối nón (N) nhỏ nhất thì mặt phẳng qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của (N) có phương trình 2x + by + cz + d = 0. Tính T = b + c + d.

Nếu $\underset{0}{\overset{1}{\int }}\left[f\left(x\right)+2x\right]\text{d}x=2$  thì $\underset{0}{\overset{1}{\int }}f\left(x\right)\text{d}x$  bằng

Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $f\left[f\left(\left|x+1\right|\right)-2\right]=m$  có 10 nghiệm phân biệt thuộc đoạn [-3;3]?

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 2a. Khoảng cách từ điểm B đến mặt phẳng (ACC’A’) bằng

Trong không gian Oxyz, vectơ $\overrightarrow{n}=\left(1;-1;-3\right)$  là một vectơ pháp tuyến của mặt phẳng nào sau đây?

Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi M là trung điểm của BC. Khi quay tam giác ABC xung quanh trục AM thì đường gấp khúc ABC tạo thành một hình nón. Tính diện tích xung quanh của hình nón đó

Cho số phức z thỏa mãn (1 – 3i)z + 1 + 7i = 0. Tổng phần thực và phần ảo của z là

Cho hàm số $y=a{x}^4+b{x}^2+c\left(a,b,c\in ℝ\right)$  có đồ thị là đường cong như hình vẽ.

Giá trị cực tiểu của hàm số đã cho là

Họ các nguyên hàm của hàm số $f\left(x\right)={\text{e}}^{2x+3}$  là