Cho các số phức z, w, u thỏa mãn , là số thuần ảo và \. Giá trị nhỏ nhất của thuộc khoảng nào sau đây?
A. (0;5]
B. (5;8)
C. [8;10)
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Đầu tiên ta gọi lần lượt là các điểm biểu diễn số phức z, w, u trên mặt phẳng tọa độ Oxy.
Khi đó ta có:
Đặt , khi đó
(2)
Thế vào (2) kết hợp biến đổi đại số, ta được .
Suy ra , tức thuộc đường tròn tâm , bán kính R = 1.
Khi đó ta luôn có:
Gọi là điểm đối xứng với qua (d), khi đó ta suy ra tức .
Khi đó ta có hình vẽ như sau:
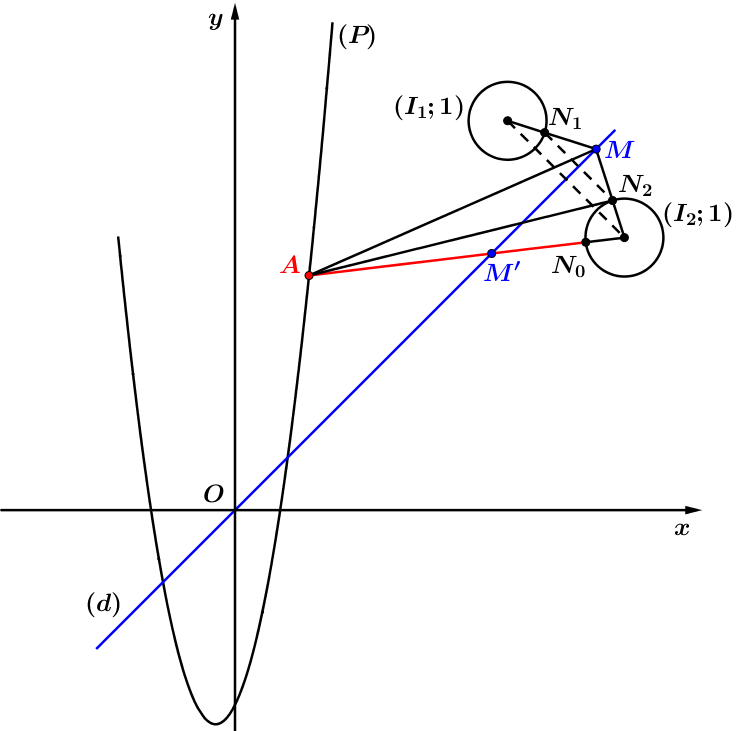
Từ hình vẽ, ta dễ dàng suy ra:
Mặt khác theo bất đẳng thức đường gấp khúc ta luôn có: nên khi tức khi và chỉ khi min. Lúc này ta quy về bài toán đơn giản hơn như sau:
“Cho và , khi ấy tìm giá trị nhỏ nhất của đoạn thẳng ”.
Lúc này ta có: .
Chạy TABLE ta suy ra .
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên.
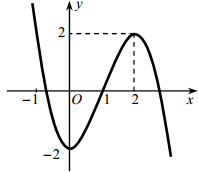
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(x) = m có ba nghiệm thực phân biệt?
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng
Cho hàm số . Biết rằng tập hợp tất cả các giá trị thực của tham số m để hàm số có số điểm cực tiểu nhiều nhất là . Giá trị của biểu thức thuộc khoảng nào sau đây?
Trong không gian Oxyz, cho điểm A (1;2;3). Điểm đối xứng với A qua mặt phẳng (Oyz) có tọa độ là
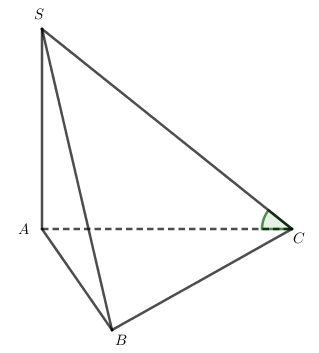
Cho khối chóp S.ABC có đáy là tam giác vuông cân tại A, AB = 2, SA vuông góc với đáy và SA = 3 (tham khảo hình bên).
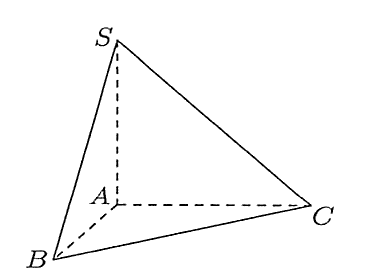
Thể tích khối chóp đã cho bằng
Một cái ly làm bằng thủy tinh, có hình dạng là khối nón cụt và các kích thước như hình vẽ. Phần rỗng bên trong có thiết diện qua trục là Parabol.
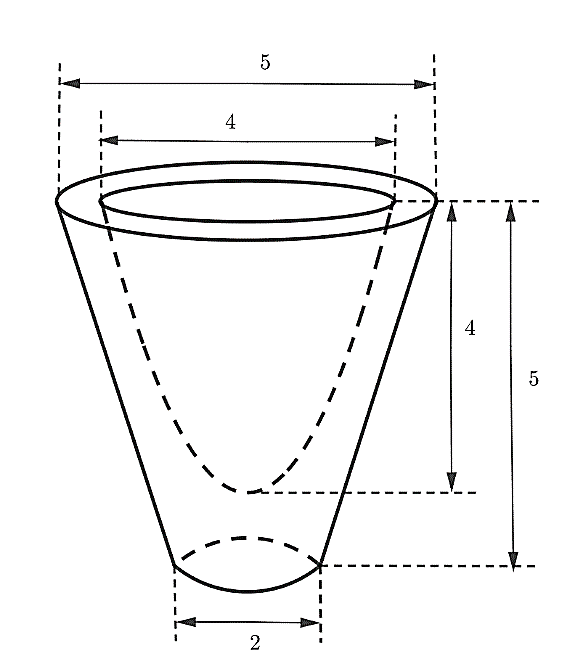
Thể tích khối thủy tinh bằng bao nhiêu?
Cho hình chóp S.ABC có ; tam giác ABC đều cạnh a và SA = a. Tìm góc giữa SC và mặt phẳng (ABC).
Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn là một đường tròn. Tâm của đường tròn đó có tọa độ là
Cho một tổ có 15 thành viên. Số cách chọn ra 2 người lần lượt làm tổ trưởng và tổ phó là
Giải bóng đá Mini cấp trường của một trường THPT, có 16 đội đăng kí tham dự trong đó có 3 đội 12A1, 12A2 và 12A3. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng (mỗi bảng 4 đội) để đá vòng loại. Tính xác suất để 3 đội của 3 lớp 12A1, 12A2 và 12A3 nằm ở 3 bảng khác nhau.
Cho hàm số có đồ thị là đường cong trong hình bên dưới.
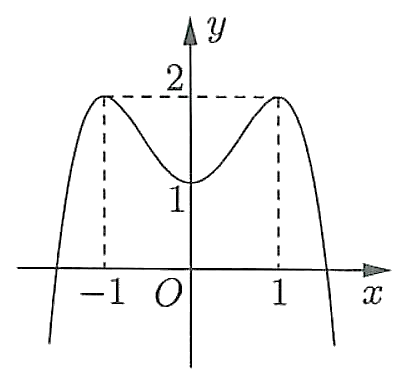
Điểm cực tiểu của hàm số đã cho là
Cho hàm số có đồ thi là đường cong trong hình bên.
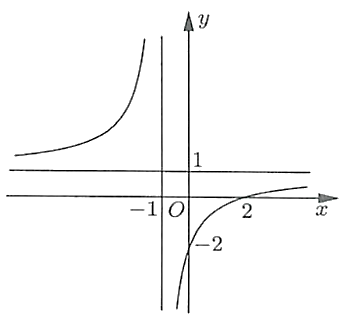
Toạ độ giao điểm của đồ thị hàm số đã cho và trục tung là:
Trong không gian Oxyz, cho hai điểm A(0;0;10) và . Xét các điểm M thay đổi sao cho tam giác OAM không phải là tam giác nhọn và có diện tích bằng 20. Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?