Cho đường tròn (O) đường kính AB. lấy điểm C thuộc (O) (C khác A và B tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với đường tròn (O) (D là tiếp điểm khác B).
1) Chứng minh tứ giác BODK nội tiếp.
2) Biết OK cắt BD tại I. Chứng minh rằng và KC.KA = KI.KO.
3) Gọi E là trung điểm của AC, kẻ đường kính CF của đường tròn (O), FE cắt AI tại H. Chứng minh rằng H là trung điểm của AI.
 Giải bởi Vietjack
Giải bởi Vietjack
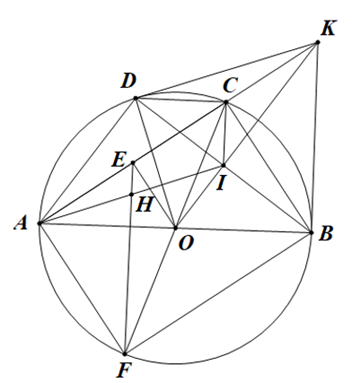
1) Ta có
.
Do đó tứ giác BODK nội tiếp.
2) Ta có KB = KD (tính chất hai tiếp tuyến cắt nhau).
Ta lại có OB = OD nên OK là đường trung trực của BD
Suy ra
Xét tam giác ABK vuông tại B nên
Xét tam giác OBK vuông tại B nên
Suy ra (đpcm).3) Xét KCI và KOA ta có góc K chung, .
Suy ra . Suy ra . (*)
Xét tam giác ACF và BAK có (1)
Mà tam giác OAC cân tại O nên (2)
Từ (1) và (2) suy ra
Suy ra .
Xét tam giác AEF và BOK ta có và
Nên suy ra (cùng bù với ) (**)
Từ (*) và (**) ta có suy ra EF // CI.
Xét tam giác ACI có E là trung điểm của AC và EF // CI nên H là trung điểm của AI.
Một mảnh vườn hình chữ nhật có diện tích 600m2 . Biết rằng nếu tăng chiều dài 10m và giảm chiều rộng 5m thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng .
a) Tính .
b) Trên cạnh BC lấy điểm M sao cho MC = 2MB, tính diện tích tam giác AMC.
Cho parabol (P): y - x2 và đường thẳng (d): y = x - 2.
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục toạ độ Oxy.
b) Tìm toạ độ giao điểm của Parabol (P) và đường thẳng (d) bằng phép tính.
Cho phương trình x2 - 2x + m - 3 = 0 (m là tham số).
a) Giải phương trình khi m = 0.
b) Tìm m để phương trình có hai nghiệm x1 ; x2 sao cho biểu thức đạt giá trị nhỏ nhất.
Cho biểu thức với .
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P khi x = 4.