Phương trình ${\left( {3 + \sqrt 5 } \right)^x} + {\left( {3 - \sqrt 5 } \right)^x} = 3 \cdot {2^x}$ có hai nghiệm ${x_1};{x_2}$. Tính giá trị biểu thức $A = x_1^2 + x_2^2$.
Giải bởi Vietjack
Ta có \[\left( {3 + \sqrt 5 } \right)\left( {3 - \sqrt 5 } \right) = 4 \Leftrightarrow \frac{{3 + \sqrt 5 }}{2} \cdot \frac{{3 - \sqrt 5 }}{2} = 1 \Leftrightarrow \frac{{3 - \sqrt 5 }}{2} = {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^{ - 1}}.\]
Khi đó ${\left( {3 + \sqrt 5 } \right)^x} + {\left( {3 - \sqrt 5 } \right)^x} = 3 \cdot {2^x}$
$ \Leftrightarrow {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^x} + {\left( {\frac{{3 - \sqrt 5 }}{2}} \right)^x} = 3$ (chia hai vế cho ${2^x}$)
$ \Leftrightarrow {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^x} + {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^{ - x}} = 3$
\[ \Leftrightarrow {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^{2x}} - 3 \cdot {\left( {\frac{{3 + \sqrt 5 }}{2}} \right)^x} + 1 = 0\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{{\left( {\frac{{3 + \sqrt 5 }}{2}} \right)}^x} = \frac{{3 + \sqrt 5 }}{2}} \\
{{{\left( {\frac{{3 + \sqrt 5 }}{2}} \right)}^x} = \frac{{3 - \sqrt 5 }}{2}}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 1} \\
{x = - 1}
\end{array}.} \right.\]
Vậy $A = 2.$
Cho $a$ là số thực dương khác $1$. Khi đó $\sqrt[8]{{{a^3}}}$ bằng
Cho ${4^x} + {4^{ - x}} = 7$. Khi đó biểu thức $P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + 4 \cdot {2^x} + 4 \cdot {2^{ - x}}}} = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản và $a,b \in \mathbb{Z}$. Tích $ab$ có giá trị bằng
Nếu $m$ là số nguyên dương, biểu thức nào sau đây không bằng với ${\left( {{2^4}} \right)^m}$?
Tính đạo hàm của các hàm số sau:
a) $y = \left( {2{x^3} - 5x} \right) \cdot {3^x}$; b) $y = \sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)$.
Với $a,b$ là các số thực dương tùy ý và $a \ne 1$, ${\log _{{a^5}}}b$ bằng
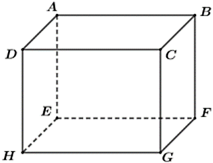
Cho hình hộp chữ nhật \[ABCD.EFGH\]. Xác định số đo góc giữa hai đường thẳng $AE$ và $CD$.
Cho hình chóp \[S.ABC\] có \[SA \bot \left( {ABC} \right)\] (như hình vẽ dưới).
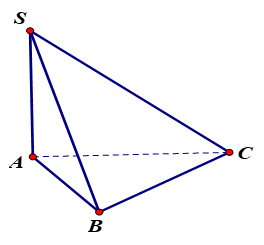
Hình chiếu của \[SC\] lên mặt phẳng \[\left( {ABC} \right)\] là
Cho $a$ là số thực dương khác $1.$ Giá trị của ${a^{{{\log }_{\sqrt a }}4}}$ là
Cho ${\log _2}x = \sqrt 2 $. Giá trị của biểu thức $A = {\log _2}{x^2} + {\log _{\frac{1}{2}}}{x^3} + {\log _4}x$ bằng
Cho đường thẳng $a$ vuông góc với mặt phẳng $\left( P \right)$, đường thẳng $b$ vuông góc với đường thẳng $a$. Phát biểu nào sau đây là đúng?
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$, $SA \bot \left( {ABCD} \right)$, $AD = 2a,\,AB = BC = a$. Chứng minh rằng $DC \bot \left( {SAC} \right)$.
