Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi, $SA = SC$. Khẳng định nào sau đây đúng?
A. Mặt phẳng \[\left( {SBD} \right)\] vuông góc với mặt phẳng $\left( {ABCD} \right)$.
B. Mặt phẳng $\left( {SBC} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.
C. Mặt phẳng $\left( {SAD} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.
D. Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.
Giải bởi Vietjack
Chọn A
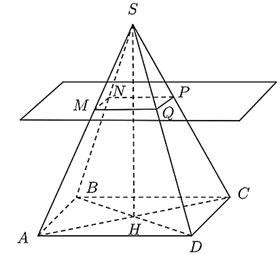
Cho hình chóp tứ giác đều $S.ABCD$. Cắt hình chóp bởi mặt phẳng song song với đáy và cắt tất cả các cạnh bên của hình chóp thì ta được
Cho hai đường thẳng \[{d_1}\] và ${d_2}$ chéo nhau. Mệnh đề nào sau đây đúng?
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\] đáy \[ABCD\] là hình thoi. Góc \[BAC\] là một góc phẳng của góc nhị diện nào sau đây?
Cho $x$, $y$ là hai số thực dương khác \[1\] và $m$, $n$ là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Hãy chọn khẳng định đúng?
Cho $0 < a \ne 1,\,M > 0$ và $\alpha $ là số thực tùy ý. Mệnh đề nào sau đây là sai?
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh $a$. Gọi \[\alpha \] là góc giữa \[AC\] và mặt phẳng \[\left( {A'BCD'} \right).\] Chọn khẳng định đúng trong các khẳng định sau.
Cho khối chóp có diện tích đáy $B$ và chiều cao $h$. Thể tích $V$ của khối chóp đã cho được tính theo công thức nào dưới đây?
Cho \[a > 0\], \[b > 0\] và \[{a^2} + {b^2} = 7ab\]. Đẳng thức nào dưới đây là đúng?
Cho các số dương \[a \ne 1\] và các số thực \[\alpha \], \[\beta \]. Đẳng thức nào sau đây đúng?
