Cho đường tròn \(\left( {O;R} \right)\) có đường kính \(AB,\) đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại điểm \(A,\) điểm \(C\) di động trên \(d\) sao cho \(C\) không trùng với \(A\) và \(CA > R.\) Từ \(C\) kẻ tiếp tuyến \(CD\) của đường tròn \(\left( O \right)\) \((D\) là tiếp điểm và \(D\) không trùng với \(A).\)
1) Chứng minh tứ giác \(AODC\) nội tiếp đường tròn.
2) Gọi \(H\) là giao điểm của \(AD\) và \(OC,\,\,BC\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(K\left( {K \ne B} \right),\) đoạn thẳng \(CH\) cắt đường tròn \(\left( O \right)\) tại điểm \(I.\) Chứng minh rằng \(IC \cdot IO = IH \cdot CO\) và \(\widehat {CKH} = 2 \cdot \widehat {IAO}.\)
Giải bởi Vietjack
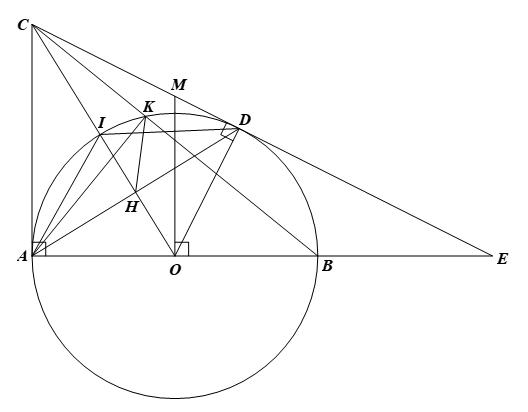
1) ⦁ Vì \(CA,CD\) là các tiếp tuyến của đường tròn \(\left( O \right)\), nên \(CA \bot OA\) tại \(A\) và \(AD \bot OD\) tại \(D\) hay \(\widehat {CAO} = 90^\circ ;\,\,\widehat {CDO} = 90^\circ .\)
Do đó hai điểm \(A,\,\,D\) nằm trên đường tròn đường kính \(CO.\)
Vậy tứ giác \(AODC\) nội tiếp được đường tròn đường kính \(CO.\)
2) * Chứng minh \(IC \cdot IO = IH \cdot CO\)
⦁ Do \(C\) là giao của hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right),\) nên \(OC\) là phân giác của góc \(AOD\) hay \(\widehat {AOI} = \widehat {DOI}.\) Suy ra nên \[\widehat {ADI} = \widehat {IAD}\,\,\,\left( 1 \right)\] (hai góc nội tiếp chắn hai cung bằng nhau của đường tròn \(\left( O \right)).\)
Ta có \(\widehat {CAI} + \widehat {IAO} = 90^\circ \) nên \(\widehat {CAI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 2 \right)\)
Xét \(\Delta OAI\) cân tại \(O\) (do \(OA = OI)\) nên \(\widehat {IAO} = \widehat {AIO} = \frac{{180^\circ - \widehat {AOI}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOI}.\)
Lại có \(\widehat {ADI} = \frac{1}{2}\widehat {AOI}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AI\) của đường tròn \(\left( O \right)).\)
Do đó \(\widehat {IAO} = 90^\circ - \widehat {ADI}\) hay \(\widehat {ADI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) và \(\left( 3 \right)\) suy ra \[\widehat {CAI} = \widehat {IAD}\,\,\left( { = \widehat {ADI}} \right)\] hay \(AI\) là phân giác của \(\widehat {CAH}.\)
Xét \(\Delta CAH\) có \[AI\] là phân giác của \(\widehat {CAH}\) nên: \(\frac{{IC}}{{IH}} = \frac{{AC}}{{AH}}.\,\,\,\left( 4 \right)\)
⦁ Ta có \(OA = OD\) và \(CA = CD\) (tính chất hai tiếp tuyến cắt nhau) nên \(OC\) là đường trung trực của \(AD\) hay \(AH \bot OC\)
Xét \(\Delta AHO\) vuông tại \(H,\) ta có \(\sin \widehat {AOH} = \frac{{AH}}{{AO}}.\)
Xét \(\Delta ACO\) vuông tại \(A,\) ta có \(\sin \widehat {AOH} = \sin \widehat {AOC} = \frac{{AC}}{{CO}}.\)
Do đó \(\frac{{AH}}{{AO}} = \frac{{AC}}{{CO}}\) hay \(\frac{{AC}}{{AH}} = \frac{{CO}}{{AO}} = \frac{{CO}}{{OI}}\,\,\,\left( 5 \right)\) (do \(OA = OI)\)
Từ \[\left( 4 \right)\] và \(\left( 5 \right)\) suy ra: \(\frac{{IC}}{{IH}} = \frac{{CO}}{{OI}}\) hay \(IC \cdot OI = IH \cdot CO.\)
* Chứng minh \(\widehat {CKH} = 2\widehat {IAO}\)
Nối \(AK,\) ta có \(\widehat {AKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(AK \bot BC.\)
Xét \(\Delta CAK\) và \(\Delta ABC\) có: \(\widehat {AKC} = \widehat {BAC} = 90^\circ \) và \(\widehat {ACB}\) là góc chung
Do đó (g.g), suy ra \(\frac{{CA}}{{CB}} = \frac{{AK}}{{CA}}\) hay \(C{A^2} = CK \cdot CB.\)
Tương tự, ta có (g.g) suy ra \(\frac{{CA}}{{CO}} = \frac{{CH}}{{CA}}\) hay \(C{A^2} = CH \cdot CO.\)
Suy ra \(CK \cdot CB = CH \cdot CO\) nên \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Xét \(\Delta CKH\) và \(\Delta COB\) có: \[\widehat {OCB}\] là góc chung và \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Do đó (c.g.c), suy ra \(\widehat {CKH} = \widehat {COB}\) (hai góc tương ứng).
Mặt khác \(\widehat {COB} = \widehat {IOB} = 2\widehat {IAB}\) (Góc ở tâm và góc nội tiếp cùng chắn cung \(BI)\)
Suy ra \(\widehat {CKH} = 2\widehat {IAB}\) hay \(\widehat {CKH} = 2 \cdot \widehat {IAO}.\)
3) Ta có \(OM\,{\rm{//}}\,AC\) (cùng vuông góc với \(AB)\)nên \(\widehat {COM} = \widehat {OCA}\) (hai góc so le trong).
Mà \(CO\) là tia phân giác của \(\widehat {ACD}\) (do hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right)\) cắt nhau tại \(C)\) nên \(\widehat {OCA} = \widehat {OCM}.\)
Do đó \[\widehat {COM} = \widehat {OCM}\] suy ra \[\Delta CMO\] cân tại \(M.\) Từ đó ta có \(MC = MO.\)
Xét \(\Delta ACE\) có \(MO\,{\rm{//}}\,CA\) nên theo hệ quả định lí Thalès, ta có: \[\frac{{CA}}{{MO}} = \frac{{AE}}{{OE}}.\]
Xét \(\Delta ODE\) và \(\Delta MOE\) có: \(\widehat {ODE} = \widehat {MOE} = 90^\circ \) và \(\widehat {OEM}\) là góc chung
Do đó (g.g), suy ra \(\frac{{OE}}{{ME}} = \frac{{OD}}{{MO}}\) hay \(\frac{{OE}}{{OD}} = \frac{{ME}}{{MO}}.\)
Khi đó: \(T = 9 \cdot \frac{{CA}}{{CM}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{CA}}{{MO}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{AE}}{{OE}} + \frac{{OE}}{{OD}} = 9 \cdot \frac{{OE + OA}}{{OE}} + \frac{{OE}}{{OD}}\)
\( = 9 \cdot \left( {1 + \frac{{OA}}{{OE}}} \right) + \frac{{OE}}{{OA}}\)\( = 9 + \left( {9 \cdot \frac{{OA}}{{OE}} + \frac{{OE}}{{OA}}} \right)\) \[\mathop \ge \limits^{{\rm{B\ST Cauchy}}} \]\[9 + 2\sqrt {9 \cdot \frac{{OA}}{{OE}} \cdot \frac{{OE}}{{OA}}} = 15.\]
Dấu “=" xảy ra khi và chỉ khi \(\frac{{OA}}{{OE}} = \frac{{OE}}{{OA}}\) hay \(9O{A^2} = O{E^2},\) tức là \(OE = 3 \cdot OA = 3R.\)
Dễ dàng chứng minh được (g.g)
Suy ra \(\frac{{OE}}{{CE}} = \frac{{OD}}{{CA}}\) hay \(\frac{{CE}}{{CA}} = \frac{{OE}}{{OD}} = \frac{{3R}}{R} = 3\) hay \(CE = 3CA.\)
Áp dụng định lí Pythagore cho \(\Delta ACE\) vuông tại \(A,\) ta có: \(C{E^2} - C{A^2} = A{E^2}\)
Suy ra \(9 \cdot C{A^2} - C{A^2} = {\left( {AO + OE} \right)^2}\)
Hay \(8C{A^2} = {\left( {R + 3R} \right)^2}\) nên \(8C{A^2} = 16{R^2},\) suy ra \(CA = R\sqrt 2 .\)
Vây điểm \(C\) cách \(A\) một khoảng bằng \(R\sqrt 2 \) thì biểu thức \(T\) đạt giá trị nhỏ nhất bằng \(15.\)
Nhân ngày Quốc tế thiếu nhi, cô chủ nhiệm lớp đi mua bút làm quà tặng cho học sinh. Cửa hàng cô đến mua đang có chương trình ưu đãi như sau: giảm giá \(20{\rm{\% }}\) so với giá niêm yết từ cái thứ 1 đến cái thứ 30 cho mỗi cái bút; từ cái thứ 31 trở đi được áp dụng mức giảm giá tiếp theo là \(40{\rm{\% }}\) so với giá niêm yết cho mỗi cái bút.
1) Cô mua 40 cái bút hết \[900{\rm{ }}000\] đồng. Tính giá niêm yết của một cái bút.
Điều kiện xác định của biểu thức \(P\left( x \right) = \sqrt {x - 10} \) là:
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - 5y = 16}\\{3x + 2y = - 3.}\end{array}} \right.\)
Cho biểu thức \(A = \frac{{3\sqrt x + 1}}{{\sqrt x + 3}}\left( {1 + \frac{1}{{\sqrt x + 2}}} \right) + \frac{9}{{\sqrt x + 2}},\) với \(x \ge 0.\)
1) Rút gọn biểu thức \(A.\)
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 4x - m - 1.\)
1) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 2.\)
Cho \(a,\,\,b,\,\,c\) là các số thực dương thỏa mãn điều kiện \(a + b + c = 3.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{b}{{{a^2} + 1}} + \frac{c}{{{b^2} + 1}} + \frac{a}{{{c^2} + 1}} + \frac{1}{4}\left( {ab + bc + ca} \right).\)
