Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như Hình 2. Giá trị nhỏ nhất của hàm số trên khoảng \(( - 2; + \infty )\) là
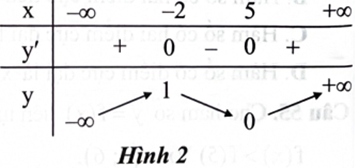
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị lớn nhất của hàm số trên đoạn \([ - 2;2]\) là
![Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị lớn nhất của hàm số trên đoạn \([ - 2;2]\) là A. 2. B. -1. C. 1. D. -3. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid1-1726996562.png)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như Hình 2. Giá trị lớn nhất của hàm số trên khoảng \(( - \infty ;5)\) là
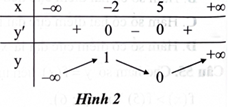
Cho hàm số \(y = f(x)\) có đồ thị đạo hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) như hình bên. Giá trị lớn nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn \([ - 1;2]\) bằng
![Cho hàm số \(y = f(x)\) có đồ thị đạo hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) như hình bên. Giá trị lớn nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn \([ - 1;2]\) bằng A. \(f( - 1).\) B. \({\rm{f}}(0).\) C. \({\rm{f}}(1).\) D. \({\rm{f}}(2).\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid5-1726997136.png)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị nhỏ nhất của hàm số trên đoạn \([ - 2;2]\) là
![Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị nhỏ nhất của hàm số trên đoạn \([ - 2;2]\) là A. -2. B. -1. C. 1. D. -3. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid0-1726996503.png)
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
![Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau: Giá trị nhỏ nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn [8; 12] bằng A. \({\rm{f}}(8).\) B. \({\rm{f}}(10).\) C. \({\rm{f}}(11).\) D. \({\rm{f}}(12).\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid4-1726997076.png)
Giá trị nhỏ nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn [8; 12] bằng