Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A
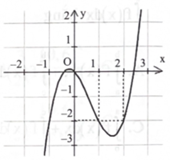
Cho hàm số \(y = f(x)\) có đồ thị như hình bên và đạo hàm \({{\rm{f}}^\prime }({\rm{x}})\) liên tục trên \(\mathbb{R}.\) Giá trị của biểu thức \(\int_1^2 {{{\rm{f}}^\prime }} ({\rm{x}}){\rm{dx}}\) bằng