 Giải bởi Vietjack
Giải bởi Vietjack
Diện tích của đáy bể là: \(S = \frac{V}{h} = \frac{{96\,\,000}}{{60}} = 1\,600\) cm2 \( = 0,16\) m2.
Gọi chiều dài đáy của bể là \(x\) (m, \(x > 0\)).
Chiều rộng đáy của bể là \(\frac{{0,16}}{x}\) (m).
Chi phí để hoàn thành bể cá là:
\(F\left( x \right) = 0,16 \cdot 100\,000 + 2 \cdot 0,6 \cdot x \cdot 70\,000 + 2 \cdot 0,6 \cdot \frac{{0,16}}{x} \cdot 70\,000\)
\( = 16\,000 + 84\,000x + \frac{{13\,440}}{x}\)(đồng).
Xét hàm số \(F\left( x \right) = 16\,000 + 84\,000x + \frac{{13\,440}}{x}\) với \(x \in \left( {0;\, + \infty } \right)\).
Ta có: \(F'\left( x \right) = 84\,000 - \frac{{13\,440}}{{{x^2}}}\). Trên khoảng \(\left( {0; + \infty } \right)\), \(F'\left( x \right) = 0 \Leftrightarrow x = 0,4\).
Bảng biến thiên của hàm số \(F\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) như sau:
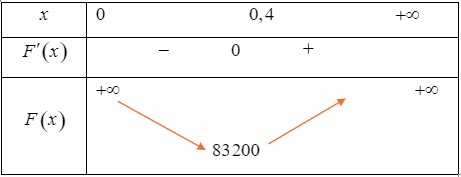
Căn cứ vào bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} F\left( x \right) = F\left( {0,4} \right) = 83\,200\).
Vậy chi phí thấp nhất để hoàn thành bể cá là \(83\,200\) đồng = \(83,2\) nghìn đồng.
Đáp số: \(83,2\).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
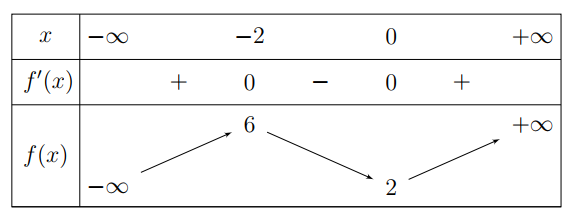
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
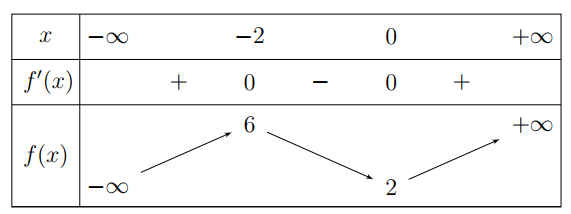
Câu 1. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
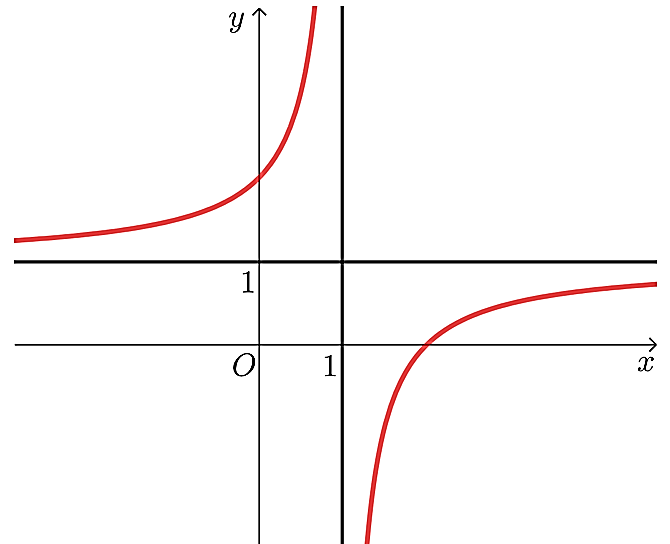
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
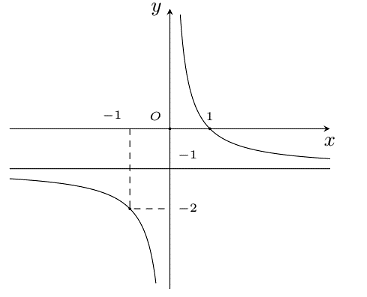
Phát biểu nào sau đây là đúng?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \frac{{x + m}}{{x + 2024}}\) đồng biến trên từng khoảng xác định của nó?
Cho hình hộp \(ABCD.A'B'C'D'\).
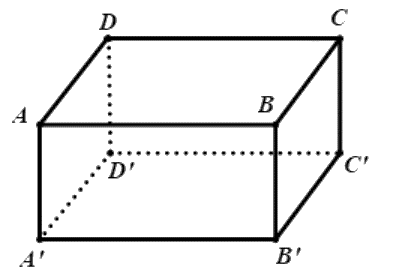
Tổng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) bằng vectơ nào sau đây?
Cho hình hộp \(ABCD.A'B'C'D'\) có tất cả các cạnh đều bằng \(a\) và \(\widehat {ABC} = \widehat {A'AB} = \widehat {A'AD} = 60^\circ \). Khi đó:
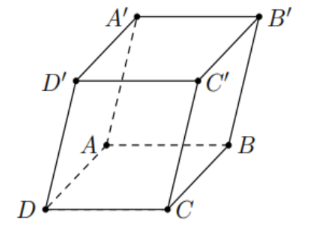
a) \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = a\).
b) \(\overrightarrow {AA'} \cdot \overrightarrow {AB} = {a^2}\).
c) \(\left| {\overrightarrow {D'A'} + \overrightarrow {D'C'} } \right| = a\sqrt 3 \).
d) \(\overrightarrow {AA'} \cdot \overrightarrow {AC} = {a^2}\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Đường cong trong hình dưới là đồ thị của hàm số nào trong bốn hàm số sau đây?
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 4x + 7}}{{x + 1}}\).
a) Hàm số đã cho nghịch biến trên từng khoảng \(\left( { - 3; - 1} \right)\) và \(\left( { - 1;1} \right)\).
b) Giá trị cực tiểu của hàm số đã cho là \( - 2\).
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng \(x = - 1\), tiệm cận xiên là đường thẳng \(y = x + 3\).
d) Đồ thị hàm số \(y = f\left( x \right)\) đi qua 6 điểm có tọa độ nguyên.
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 1;\,3} \right]\) và có đồ thị như hình dưới đây.
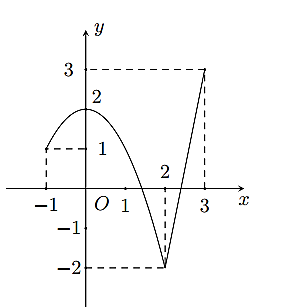
Phát biểu nào sau đây là đúng?
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.
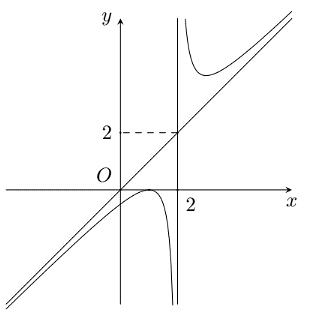
Tâm đối xứng của đồ thị hàm số có tọa độ là
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) (tham khảo hình vẽ). Khi đó:
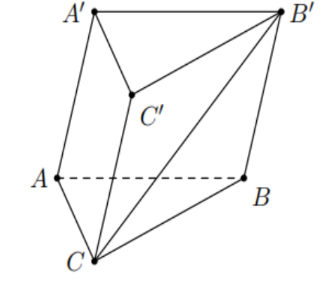
a) \(\overrightarrow {BA} + \overrightarrow {A'C'} = \overrightarrow {BC} \).
b) \(\overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {B'C'} = \overrightarrow {AC'} \).
c) \(\left( {\overrightarrow {BC} ,\,\overrightarrow {AA'} } \right) = \left( {\overrightarrow {BC} ,\,\overrightarrow {BB'} } \right) = \left( {\overrightarrow {BC} ,\,\overrightarrow {CC'} } \right)\).
d) \(\overrightarrow {B'C} \cdot \overrightarrow {BA} = \left| {\overrightarrow {B'C} } \right| \cdot \left| {\overrightarrow {BA} } \right| \cdot \cos \widehat {A'CB'}\).