Cho tam giác \[ABC\] vuông tại \[C\] có \[AC = 1,2{\rm{\;cm}},\,\,AB = 1,5{\rm{\;cm}}.\] Tỉ số lượng giác \[\tan B\] là
A. \[\tan B = \frac{{4\sqrt {41} }}{{41}}.\]
B. \[\tan B = \frac{4}{3}.\]
C. \[\tan B = \frac{3}{4}.\]
D. \[\tan B = \frac{4}{5}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[C\], ta được:
\[B{C^2} = A{B^2} - A{C^2} = 1,{5^2} - 1,{2^2} = 0,81.\]
Suy ra \[BC = 0,9{\rm{\;(cm)}}{\rm{.}}\]
Vì tam giác \[ABC\] vuông tại \[C\] nên \[\tan B = \frac{{AC}}{{BC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\]
Vậy ta chọn phương án B.
III. Vận dụng
Một mảnh vườn hình chữ nhật có chiều dài \[30{\rm{\;m}},\] chiều rộng \[10\sqrt 3 {\rm{\;m}}.\] Khi đó góc giữa đường chéo và chiều dài của mảnh vườn bằng
Một cột đèn cao \[7\] m có bóng trên mặt đất dài \[4\] m, gần đó có một tòa nhà cao tầng có bóng trên mặt đất dài \[80\] m (hình vẽ).
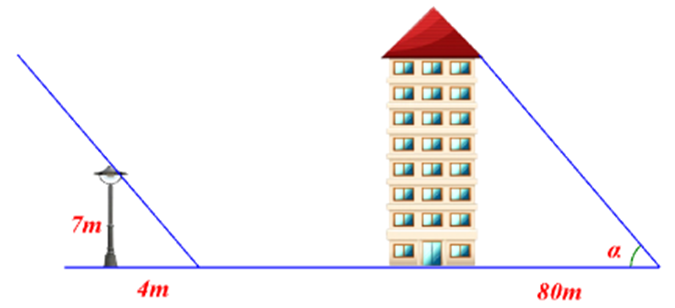
Em hãy cho biết tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao \[2\] m?
Một máy bay đang bay ở độ cao \[12\] km, khi hạ cánh xuống mặt đất, đường đi của máy bay tạo với mặt đất một góc nghiêng \[\alpha .\] Nếu đường bay của máy bay dài \[320\] km thì góc nghiêng \[\alpha \] gần nhất với
Giá trị của biểu thức \[I = \frac{{\sin 32^\circ }}{{\cos 58^\circ }}\] bằng
Cho \[\alpha ,\beta \] là hai góc phụ nhau. Kết luận nào sau đây đúng?
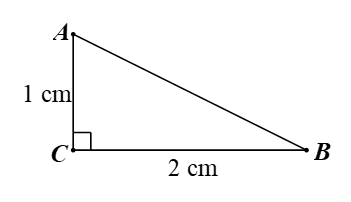
Cho tam giác \[ABC\] vuông tại \[C\] có \[AC = 1{\rm{\;cm}},\,\,BC = 2{\rm{\;cm}}.\] Tỉ số lượng giác \[\sin B,\,\,\cos B\] là
Số đo góc nhọn \[\alpha \] thỏa mãn \[\sin \alpha = 0,75\] gần nhất với
Cho tam giác vuông có góc nhọn \[\alpha .\] Khẳng định nào sau đây sai?
Cho tam giác \[DEF\] vuông tại \[D\] có \[DE = \sqrt 2 {\rm{\;cm}},\,\,EF = \sqrt {10} {\rm{\;cm}}.\] Tỉ số lượng giác \[\cot E\] là
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A.\] Trong các khẳng định sau, khẳng định nào đúng?