Cho \[\alpha \] là góc nhọn thỏa mãn \[\tan \alpha = \frac{1}{6}.\] Khi đó \[\cot \alpha \] bằng
A. \[\cot \alpha = \frac{1}{6}.\]
B. \[\cot \alpha = - \frac{1}{6}.\]
C. \[\cot \alpha = - 6.\]
D. \[\cot \alpha = 6.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có \[\cot \alpha = \frac{1}{{\tan \alpha }} = 1:\frac{1}{6} = 1 \cdot 6 = 6.\]
Vậy ta chọn phương án D.
Nếu tam giác \[MNP\] vuông tại \[M\] có \[NP = 7,\,\,\sin P = \frac{2}{9}\] thì \[MN\] bằng
III. Vận dụng
Cho tam giác \[ABC\] vuông tại \[A\] có \[AH\] là đường cao. Biết \[AB = 10\] cm, \[BH = 5\] cm. Tỉ số lượng giác \[\cos C\] bằng
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (hình vẽ), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1{\rm{\;\;}}225\] m và dùng giác kế ngắm xác định được \[\widehat {ABC} = 75^\circ ;\,\,\widehat {ACB} = 65^\circ .\]

Khi đó khoảng cách \[AC\] khoảng bao nhiêu mét?
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 70^\circ \) và biểu thức:
\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\].
Giá trị của biểu thức \(A\) là
Sử dụng máy tính cầm tay, tính giá trị của biểu thức \[M = \sin 35^\circ 12' + \cot 20^\circ 25'\] rồi làm tròn kết quả đến hàng phần trăm ta được
Một thanh chống dài \[2,5\] m hợp với tường một góc \[40^\circ \] để chống một tấm nhựa che nắng (hình vẽ).
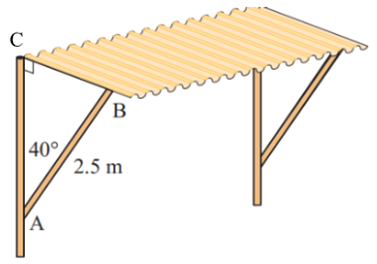
Hỏi khoảng cách từ tường đến vị trí đặt đầu thanh chống trên tấm nhựa là khoảng bao nhiêu mét?
Cho \[\alpha ,\,\,\beta \] là số đo các góc nhọn của một tam giác vuông. Khẳng định nào sau đây là đúng?
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 6{\rm{\;cm}},\,\,AC = 8{\rm{\;cm}}.\] Khẳng định nào sau đây sai?
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 8{\rm{\;cm}},\,\,AC = 6{\rm{\;cm}}.\] Kết quả nào sau đây là đúng?
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm}},\,\,\cos B = \frac{5}{8}.\] Kết quả nào sau đây là đúng?
Tam giác \[ABC\] vuông tại \[A\] ở hình bên mô tả cột cờ \[AB\] và bóng nắng của cột cờ trên mặt đất \[AC.\]
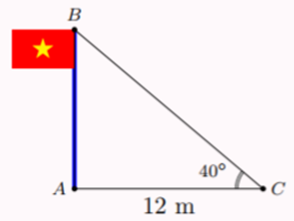
Người ta đo được độ dài \[AC = 12{\rm{\;m}}\] và \[\widehat C = 40^\circ .\] Chiều cao \[AB\] của cột cờ khi làm tròn đến hàng phần trăm là
Một cây tre cao 9 m bị gió bão làm gãy ngang thân, tạo thành một góc \(32^\circ \).
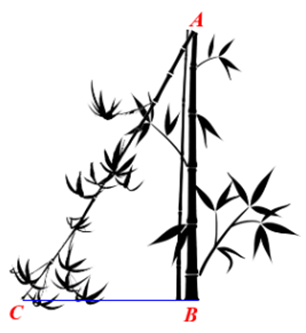
Hỏi điểm gãy \[A\] cách gốc \[B\] bao nhiêu mét?
I. Nhận biết
Cho tam giác \[DEF\] vuông tại \[E\] có góc nhọn \[F\] bằng \[\alpha .\] Khi đó \[\sin \alpha \] bằng