15 câu trắc nghiệm Toán 9 Chân trời sáng tạo Bài tập cuối chương 4 có đáp án
-
46 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho tam giác \[DEF\] vuông tại \[E\] có góc nhọn \[F\] bằng \[\alpha .\] Khi đó \[\sin \alpha \] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
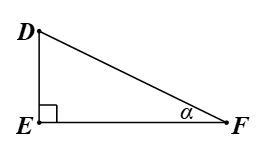
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có tam giác \[DEF\] vuông tại \[E\] nên \[\sin \alpha = \frac{{DE}}{{DF}}.\]
Vậy ta chọn phương án B.
Câu 2:
Cho \[\alpha \] là góc nhọn thỏa mãn \[\tan \alpha = \frac{1}{6}.\] Khi đó \[\cot \alpha \] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có \[\cot \alpha = \frac{1}{{\tan \alpha }} = 1:\frac{1}{6} = 1 \cdot 6 = 6.\]
Vậy ta chọn phương án D.
Câu 3:
Cho hình vẽ dưới đây.
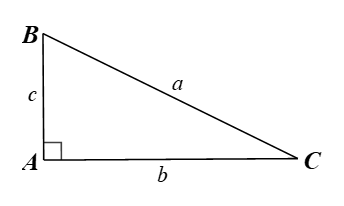
Hệ thức nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì tam giác \[ABC\] vuông tại \[A\] nên:
⦁ \[b = a\sin B = a\cos C = c\tan B = c\cot C\,;\]
⦁ \[c = a\sin C = a\cos B = c\tan B = c\cot C.\]
Vậy ta chọn phương án C.
Câu 4:
Nếu tam giác \[MNP\] vuông tại \[M\] có \[NP = 7,\,\,\sin P = \frac{2}{9}\] thì \[MN\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
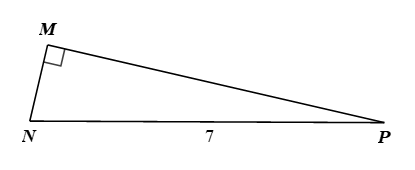
Vì tam giác \[MNP\] vuông tại \[M\] nên \[MN = NP.\sin P = 7.\frac{2}{9} = \frac{{14}}{9}.\]
Vậy ta chọn phương án D.
Câu 5:
Cho \[\alpha ,\,\,\beta \] là số đo các góc nhọn của một tam giác vuông. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Do \[\alpha ,\,\,\beta \] là số đo các góc nhọn của một tam giác vuông nên \(\alpha + \beta = 90^\circ \).
Khi đó \(\sin \alpha = \cos \beta ,\,\,\cos \alpha = \sin \beta ,\,\,\tan \alpha = \cot \beta ,\,\,\cot \alpha = \tan \beta \) và \(\tan \alpha \cdot \cot \alpha = 1\).
Do đó \(\tan \alpha - \cot \beta = \tan \alpha - \tan \alpha = 0.\)
Câu 6:
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 6{\rm{\;cm}},\,\,AC = 8{\rm{\;cm}}.\] Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D

Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[A\], ta được:
\[B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100.\] Suy ra \[AB = 10{\rm{\;cm}}.\]
Vì tam giác \[ABC\] vuông tại \[A\] nên:
⦁ \[\sin C = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}.\] Do đó phương án A là khẳng định đúng.
⦁ \[\cos C = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}.\] Do đó phương án B là khẳng định đúng.
⦁ \[\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}.\] Do đó phương án C là khẳng định đúng.
⦁ \[\cot B = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}.\] Do đó phương án D là khẳng định sai.
Vậy ta chọn phương án D.
Câu 7:
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 70^\circ \) và biểu thức:
\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\].
Giá trị của biểu thức \(A\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Với \(0^\circ < \alpha < 70^\circ \), ta có: \[90^\circ - \left( {70^\circ - \alpha } \right) = \alpha + 20^\circ ;\,\,\,90^\circ - \left( {80^\circ - \alpha } \right) = \alpha + 10^\circ .\]
Do đó:
\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\]
\[\,\,\,\,\, = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right) \cdot \cot \alpha \]
\[\,\,\,\,\, = \left( {\tan \alpha \cdot \cot \alpha } \right) \cdot \left[ {\tan \left( {\alpha + 10^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right)} \right] \cdot \left[ {\tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right)} \right]\]
\[\,\,\,\,\, = 1 \cdot 1 \cdot 1 = 1.\]
Câu 8:
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 8{\rm{\;cm}},\,\,AC = 6{\rm{\;cm}}.\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
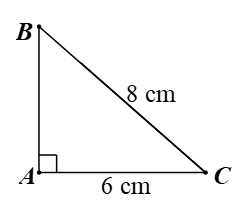
Xét tam giác \[ABC\] vuông tại \[A,\] có: \[A{B^2} + A{C^2} = B{C^2}\] (Định lí Pythagore)
Suy ra \[A{B^2} = B{C^2} - A{C^2} = {8^2} - {6^2} = 28.\]
Do đó \[AB = 2\sqrt 7 \] (cm).
Vì tam giác \[ABC\] vuông tại \[A\] nên \[\tan C = \frac{{AB}}{{AC}} = \frac{{2\sqrt 7 }}{6} = \frac{{\sqrt 7 }}{3}.\]
Do đó ta chọn phương án C.
Câu 9:
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm}},\,\,\cos B = \frac{5}{8}.\] Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B

Xét tam giác \[ABC\] vuông tại \[A\], có:
⦁ \[\cos B = \frac{{AB}}{{BC}}.\] Suy ra \[BC = \frac{{AB}}{{\cos B}} = \frac{5}{{\frac{5}{8}}} = 8\] (cm);
⦁ \[B{C^2} = A{B^2} + A{C^2}\] (theo định lí Pythagore)
Suy ra \[A{C^2} = B{C^2} - A{B^2} = {8^2} - {5^2} = 39.\] Do đó \[AC = \sqrt {39} \] (cm).
Vậy ta chọn phương án B.
Câu 10:
Tam giác \[ABC\] vuông tại \[A\] ở hình bên mô tả cột cờ \[AB\] và bóng nắng của cột cờ trên mặt đất \[AC.\]
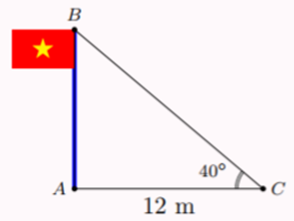
Người ta đo được độ dài \[AC = 12{\rm{\;m}}\] và \[\widehat C = 40^\circ .\] Chiều cao \[AB\] của cột cờ khi làm tròn đến hàng phần trăm là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AB = AC.\tan C = 12.\tan 40^\circ \approx 10,07\] (m).
Do đó chiều cao \[AB\] của cột cờ khoảng \[10,07\] m.
Vậy ta chọn phương án B.
Câu 11:
Sử dụng máy tính cầm tay, tính giá trị của biểu thức \[M = \sin 35^\circ 12' + \cot 20^\circ 25'\] rồi làm tròn kết quả đến hàng phần trăm ta được
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \[\cot 20^\circ 25' = \tan \left( {90^\circ - 20^\circ 25'} \right).\]
Đầu tiên, ta đưa máy tính về chế độ “độ”, sau đó ấn liên tiếp các phím
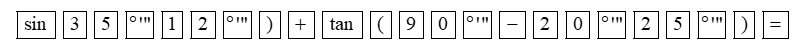
Màn hình hiện lên kết quả là \(3,262959062,\) làm tròn kết quả đến hàng phần trăm ta được: \(3,26.\)
Nghĩa là, \[M = 3,26.\]
Vậy ta chọn phương án C.
Câu 12:
Một thanh chống dài \[2,5\] m hợp với tường một góc \[40^\circ \] để chống một tấm nhựa che nắng (hình vẽ).
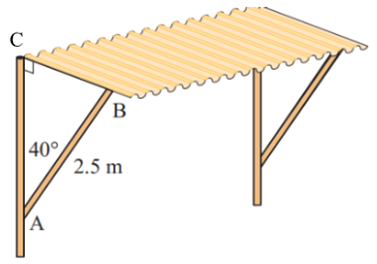
Hỏi khoảng cách từ tường đến vị trí đặt đầu thanh chống trên tấm nhựa là khoảng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo đề, ta có \[\widehat {BAC} = 40^\circ \] và \[AB = 2,5\] (m).
Vì tam giác \[ABC\] vuông tại \[C\] nên \[BC = AB.\sin \widehat {BAC} = 2,5.\sin 40^\circ \approx 1,6\] (m).
Do đó khoảng cách từ tường đến vị trí đặt đầu thanh chống trên tấm nhựa khoảng \[1,6\] mét.
Vậy ta chọn phương án A.
Câu 13:
III. Vận dụng
Cho tam giác \[ABC\] vuông tại \[A\] có \[AH\] là đường cao. Biết \[AB = 10\] cm, \[BH = 5\] cm. Tỉ số lượng giác \[\cos C\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
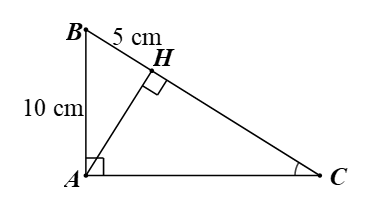
Tam giác \[ABC\] vuông tại \[A\] có: \[\widehat {B\,} + \widehat {C\,} = 90^\circ .\]
Do đó hai góc \(B\) và \(C\) phụ nhau nên \(\cos C = \sin B.\)
Tam giác \[ABC\] vuông tại \[A\] có \[AH\] là đường cao nên \[AH \bot BC\] tại \[H.\]
Xét tam giác \[ABH\] vuông tại\(H,\) theo định lí Pythagore, ta có: \(A{B^2} = A{H^2} + B{H^2}\)
Suy ra \(A{H^2} = A{B^2} - B{H^2} = {10^2} - {5^2} = 75.\) Do đó \(AH = \sqrt {75} = 5\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Ta có \[\cos C = \sin B = \frac{{AH}}{{AB}} = \frac{{5\sqrt 3 }}{{10}} = \frac{{\sqrt 3 }}{2}.\]
Vậy ta chọn phương án C.
Câu 14:
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (hình vẽ), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1{\rm{\;\;}}225\] m và dùng giác kế ngắm xác định được \[\widehat {ABC} = 75^\circ ;\,\,\widehat {ACB} = 65^\circ .\]

Khi đó khoảng cách \[AC\] khoảng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
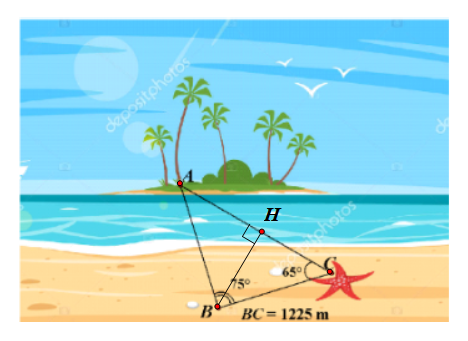
Kẻ \[BH \bot AC\] tại \[H.\]
Tam giác \[ABC,\] có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ - \left( {75^\circ + 65^\circ } \right) = 40^\circ .\]
Vì tam giác \[BCH\] vuông tại \[H\] nên:
⦁ \[BH = BC.\sin \widehat {BCH} = 1{\rm{\;\;}}225.\sin 65^\circ \] (m);
⦁ \[CH = BC.\cos \widehat {BCH} = 1{\rm{\;\;}}225.\cos 65^\circ \] (m).
Vì tam giác \[ABH\] vuông tại \[H\] nên \(BH = AH \cdot \tan \widehat {BAH}\)
Suy ra \[AH = \frac{{BH}}{{\tan \widehat {BAH}}} = \frac{{1{\rm{\;\;}}225 \cdot \sin 65^\circ }}{{\tan 40^\circ }}\] (m).
Khi đó \[AC = AH + CH = \frac{{1{\rm{\;\;}}225 \cdot \sin 65^\circ }}{{\tan 40^\circ }} + 1{\rm{\;\;}}225 \cdot \cos 65^\circ \approx 1{\rm{\;\;}}841\] (m).
Do đó khoảng cách \[AC\] khoảng \[1{\rm{\;\;}}841\] m.
Vậy ta chọn phương án B.
Câu 15:
Một cây tre cao 9 m bị gió bão làm gãy ngang thân, tạo thành một góc \(32^\circ \).
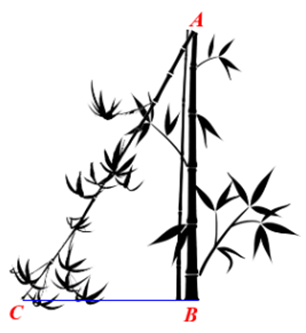
Hỏi điểm gãy \[A\] cách gốc \[B\] bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta mô hình hóa bài toán như hình vẽ bên.
Khoảng cách từ gốc cây đến điểm bị gãy là \[AB.\]
Khoảng cách từ điểm thân tre bị gãy đến ngọn cây là \[BC.\]
Khoảng cách từ ngọn cây chạm đất đến gốc là \[AC.\]
Đặt độ dài \(BC = x{\rm{\;(m)}}\,\,\left( {0 < x < 9} \right)\).
Suy ra: \(AB = 9 - x.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = BC \cdot \cos B\)
Suy ra \(9 - x = x \cdot \cos 32^\circ \)
\(9 - x \approx 0,85x\)
\(1,85x \approx 9\)
\[x \approx 4,9{\rm{\;(m)}}{\rm{.}}\]
Do đó điểm gãy cách gốc khoảng 4,9 m.
Vậy ta chọn phương án B.
