Cho tam giác \[ABC\] cân tại \[A.\] Vẽ đường tròn tâm \[O\] đường kính \[BC.\] Đường tròn \[\left( O \right)\] cắt \[AB,AC\] lần lượt tại \[I,K.\] Biết \[\widehat {BAC} = 40^\circ .\] Số đo của cung nhỏ \(IK\) bằng
A. \[30^\circ .\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
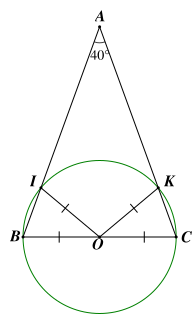
Vì tam giác \[ABC\] cân tại \[A\] nên \[\widehat {ABC} = \widehat {ACB}.\]
Tam giác\[ABC,\] có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[2\widehat {ACB} = 180^\circ - \widehat {BAC} = 180^\circ - 40^\circ = 140^\circ .\]
Do đó \[\widehat {ACB} = 70^\circ .\] Vì vậy \[\widehat {ABC} = \widehat {ACB} = 70^\circ .\]
Vì tam giác \[OBI\] cân tại \[O\] (do \[OI = OB\]) nên \[\widehat {IBO} = \widehat {BIO} = 70^\circ .\]
Tam giác \[OBI,\] có: \[\widehat {BOI} + \widehat {IBO} + \widehat {BIO} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[\widehat {BOI} = 180^\circ - \left( {\widehat {IBO} + \widehat {BIO}} \right) = 180^\circ - \left( {70^\circ + 70^\circ } \right) = 40^\circ .\]
Thực hiện tương tự, ta thu được \[\widehat {COK} = 40^\circ .\]
Đường tròn \[\left( O \right)\] có \[BC\] là đường kính hay ba điểm \(B,\,\,O,\,\,C\) thằng hàng, đo dó \[\widehat {BOC} = 180^\circ \] nên \[\widehat {BOI} + \widehat {IOK} + \widehat {COK} = 180^\circ \]
Suy ra \[\widehat {IOK} = 180^\circ - \left( {\widehat {BOI} + \widehat {COK}} \right) = 180^\circ - \left( {40^\circ + 40^\circ } \right) = 100^\circ .\]
Vậy
Do đó ta chọn phương án D.
II. Thông hiểu
Cho đường tròn \(\left( O \right)\) đi qua hai điểm \(A,\,\,B\). Biết \(\widehat {AOB} = 100^\circ \) thì số đo của cung lớn \(AB\) là
Cho đường tròn \[\left( {O;R} \right)\] có đường kính \[AB\]. Kẻ hai dây \[AC\,{\rm{//}}\,BD.\] Kết luận nào sau đây đúng?
Cho đường tròn \[\left( O \right)\] có bán kính \[R = 5{\rm{\;cm}}.\] Khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}.\] Độ dài dây \[AB\] bằng
Cho đường tròn \[\left( {O;R} \right)\] và dây cung \[MN = R\sqrt 3 .\] Kẻ \[OI \bot MN\] tại \[I.\] Số đo cung nhỏ \[MN\] bằng
Trong một trò chơi, hai bạn Thủy và Tiến cùng chạy trên một đường tròn tâm \[O\] có bán kính \[20{\rm{\;m}}\] (hình vẽ).
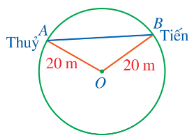
Độ dài dây \[AB\] nối vị trí của hai bạn đó không thể bằng bao nhiêu mét?
Cho đường tròn \[\left( {O;R} \right)\] và điểm \[A\] nằm trên đường tròn \[\left( {O;R} \right).\] Gọi \[H\] là điểm thuộc bán kính \[OA\] sao cho \[OH = \frac{{\sqrt 3 }}{2}OA.\] Dây \[CD\] vuông góc với \[OA\] tại \[H.\] Số đo cung lớn \[CD\] bằng
Cho hình vẽ bên.

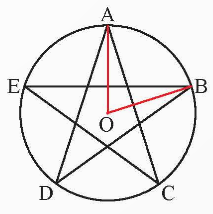
Số đo cung lớn
\[AB\] trong hình ngôi sao năm cánh đã cho bằng
I. Nhận biết
Cho đường tròn \[\left( O \right)\] đường kính \[AB\] và dây \[CD\] không đi qua tâm. Khẳng định nào sau đây là đúng?
Cho đường tròn \[\left( {O;R} \right)\] và dây \[AB.\] Trên cung nhỏ \[AB\] lấy hai điểm \[M,\,\,N\] sao cho \[AM = BN\] \[(M\] nằm trên cung nhỏ \[AN).\] Kết luận nào sau đây đúng?
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] có hai dây \[AB,CD\] vuông góc với nhau tại \[M.\] Giả sử \[AB = 16{\rm{\;cm}},CD = 12{\rm{\;cm}},MC = 2{\rm{\;cm}}.\] Kẻ \[OH \bot AB\] tại \[H,\] \[OK \bot CD\] tại \[K.\] Khi đó diện tích tứ giác \[OHMK\] bằng