Cho đường tròn \[\left( {{O_1}} \right)\] và \[\left( {{O_2}} \right)\] tiếp xúc ngoài tại \[A\] và một đường thẳng \[\left( d \right)\] tiếp xúc với \[\left( {{O_1}} \right),\,\,\left( {{O_2}} \right)\] lần lượt tại \[B,C.\] Tam giác \[ABC\] là
A. tam giác tù.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
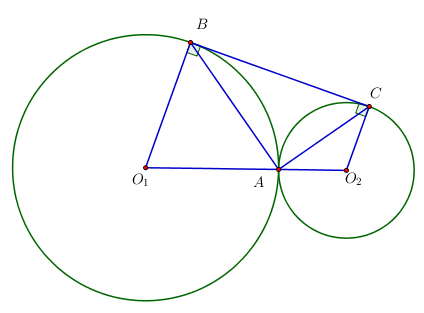
Vì \[{O_1}A = {O_1}B\] nên tam giác \[{O_1}AB\] cân tại \[{O_1}.\] Do đó \[\widehat {{O_1}AB} = \widehat {{O_1}BA}.\]
Chứng minh tương tự, ta được \[\widehat {{O_2}AC} = \widehat {{O_2}CA}.\]
Ta có đường thẳng \[\left( d \right)\] tiếp xúc với \[\left( {{O_1}} \right),\left( {{O_2}} \right)\] lần lượt tại \[B,C\] nên \[{O_1}B \bot BC\] tại \[B\] và \({O_2}C \bot BC\) tại \(C.\)
Xét tứ giác \({O_1}BC{O_2}\) ta có: \[\widehat {{O_1}} + \widehat {{O_2}} = 360^\circ - \widehat {B\,} - \widehat {C\,} = 360^\circ - 90^\circ - 90^\circ = 180^\circ \]
Suy ra \[\left( {180^\circ - \widehat {{O_1}AB} - \widehat {{O_1}BA}} \right) + \left( {180^\circ - \widehat {{O_2}AC} - \widehat {{O_2}CA}} \right) = 180^\circ \]
Khi đó \[2 \cdot \widehat {{O_1}AB} + 2 \cdot \widehat {{O_2}AC} = 180^\circ \]
Vì vậy \[2 \cdot \left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ \]
Suy ra \[\widehat {{O_1}AB} + \widehat {{O_2}AC} = 90^\circ \]
Ta có \[\widehat {{O_1}AB} + \widehat {BAC} + \widehat {{O_2}AC} = 180^\circ \]
Suy ra \[\widehat {BAC} = 180^\circ - \left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ - 90^\circ = 90^\circ .\]
Vậy tam giác \[ABC\] vuông tại \[A.\]
Do đó ta chọn phương án C.
Cho đường tròn \(\left( {I;R} \right)\) có đường kính \[12{\rm{\;dm}}\] và đường tròn \(\left( {J;R'} \right)\) có đường kính \[18{\rm{\;dm}}.\] Nếu \(IJ = 15{\rm{\;dm}}\) thì hai đường tròn \[\left( I \right),\,\,\left( J \right)\] có vị trí tương đối là
Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là
III. Vận dụng
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) với \(R < 5{\rm{\;cm}}.\) Biết \(OI = 3{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn tiếp xúc trong là
Cho hai đường tròn \[\left( {O;R} \right)\] và đường tròn \[\left( {O';r} \right)\] tiếp xúc ngoài với nhau tại \[A.\] Một đường thẳng qua \[A\] cắt \[\left( O \right)\] tại \[B\] và cắt \[\left( {O'} \right)\] tại \[C.\] Cho các nhận định sau:
(i) \[OB\,{\rm{//}}\,O'C.\]
(ii) \(OO' = R - r\) với \[R > r.\]
Khẳng định nào sau đây là đúng nhất?
III. Vận dụng
Cho đường tròn \[\left( {A;10{\rm{\;cm}}} \right),\,\,\left( {B;15{\rm{\;cm}}} \right),\,\,\left( {C;15{\rm{\;cm}}} \right)\] tiếp xúc ngoài với nhau đôi một. Hai đường tròn \[\left( B \right)\] và \[\left( C \right)\] tiếp xúc nhau tại \[A'.\] Đường tròn \[\left( A \right)\] tiếp xúc với đường tròn \[\left( B \right)\] và \[\left( C \right)\] lần lượt tại \[C',B'.\] Cho các nhận định sau:
(i) \[AA'\] là tiếp tuyến chung của hai đường tròn \[\left( B \right)\] và \[\left( C \right).\]
(ii) \[AA' = 15{\rm{\;cm}}.\]
Khẳng định nào sau đây là đúng nhất?
Cho đường tròn \[\left( O \right)\] và \[\left( {O'} \right)\] tiếp xúc ngoài tại \[A.\] Kẻ đường kính \[AB\] của đường tròn \[\left( O \right)\] và đường kính \[AC\] của đường tròn \[\left( {O'} \right).\] Gọi \[DE\] là tiếp tuyến của cả hai đường tròn \[\left( O \right)\] và \[\left( {O'} \right)\] với hai tiếp điểm \[D \in \left( O \right)\] và \[E \in \left( {O'} \right)\] \((DE\) không cắt đoạn \(O'O).\) Gọi \[M\] là giao điểm của \[BD\] và \[CE.\] Biết rằng \[\widehat {DOA} = 60^\circ \] và \[OA = 6{\rm{\;cm}}.\] Diện tích tứ giác \[ADME\] bằng
I. Nhận biết
Nếu hai đường tròn phân biệt tiếp xúc nhau thì số điểm chung của hai đường tròn là
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d.\] Chọn khẳng định đúng?
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] sao cho \[OO' < R - r\], với \[R > r.\] Khi đó ta nói </>
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r.\] Ta nói hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] ở ngoài nhau khi
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\). Biết \(OI = 7{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn ở ngoài nhau là
Cho nửa đường tròn \(\left( {O;R} \right),\) đường kính \[AB.\] Vẽ nửa đường tròn tâm \[O',\] đường kính \[AO\] (cùng phía với nửa đường tròn \[\left( O \right)\]). Một đường thẳng bất kì qua \[A\] cắt \(\left( O \right),\,\,\left( {O'} \right)\) lần lượt tại \[C,D.\] Nếu \[BC\] là tiếp tuyến của nửa đường tròn \[\left( {O'} \right)\] thì
Cho tam giác \[ABC\] vuông tại \[A,\] vẽ đường tròn \[\left( {B;BA} \right)\] và đường tròn \[\left( {C;CA} \right)\] chúng cắt nhau tại \[D\] \((D\) khác \[A\]). Kết luận nào sau đây đúng nhất?
Cho hai đường tròn \[\left( {O;4{\rm{\;cm}}} \right)\] và \[\left( {O';3{\rm{\;cm}}} \right)\] biết \[OO' = 5{\rm{\;cm}}.\] Hai đường tròn trên cắt nhau tại \[A\] và \[B.\] Độ dài \[AB\] là