Cho tam giác nhọn \[ABC\] có 3 đỉnh nằm trên đường tròn \[\left( O \right)\], đường kính \[BD\]. Biết \(\widehat {BAC} = 45^\circ \). Số đo của góc \[\widehat {CBD}\] là
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
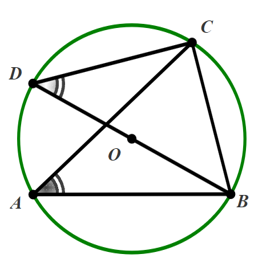
Đường tròn \[\left( O \right)\] có \[\widehat {CDB}\] và \[\widehat {CAB}\] là hai góc nội tiếp cùng chắn cung \[CB\] nên \(\widehat {CDB} = \widehat {CAB} = 45^\circ \).
Do \[\widehat {DCB}\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {DCB} = 90^\circ \).
Xét \(\Delta DCB\) có: \(\widehat {CBD} + \widehat {CDB} + \widehat {DCB} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {CBD} = 180^\circ - \widehat {CDB} - \widehat {DCB} = 180^\circ - 45^\circ - 90^\circ = 45^\circ \).
Tam giác \[ABC\] có 3 đỉnh nằm trên đường tròn \[\left( O \right)\] có \[AB = 5\,\,{\rm{cm}}\]; \[AC = 3\,\,{\rm{cm}}\]. Vẽ đường cao \[AH\] và đường kính \[AD\]. Khi đó tích \[AH.{\rm{ }}AD\] bằng
Cho tam giác \[ABC\] nhọn có \(\widehat {BAC} = 60^\circ \). Vẽ đường tròn đường kính \[BC\] tâm \[O\] cắt \[AB\], \[AC\] lần lượt tại \[D\] và \[E\]. Số đo góc \(\widehat {ODE}\) là
II. Thông hiểu
Cho đường tròn \[\left( O \right)\] và điểm \[I\] nằm ngoài \[\left( O \right)\]. Từ điểm \[I\] kẻ hai dây cung \[AB\] và \[CD\] \[(A\] nằm giữa \[I\] và \[B\], \[C\] nằm giữa \[I\] và \[D\]). Tích \[IA \cdot IB\] bằng
Cho tam giác \[ABC\] có ba góc nhọn, đường cao \[AH\] và nội tiếp đường tròn tâm \[\left( O \right)\], đường kính \[AM\]. Số đo góc \(\widehat {ABM}\) là
III. Vận dụng
Cho tam giác nhọn \[ABC\] có ba đỉnh nằm trên đường tròn \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\] và gọi\[M\] là trung điểm \[BC\]. Cho các khẳng định sau:
(i) \(OM \bot BC\).
(ii) \(OM\,{\rm{//}}\,AH\).
(iii) \(HM = \frac{{HF}}{2}\).
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
Cho tam giác \[ABC\] nhọn có ba đỉnh nằm trên đường tròn \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\]. Khẳng định nào sau đây là đúng?
I. Nhận biết
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
Cho \[\left( O \right)\], đường kính \[AB\], điểm \[D\] thuộc đường tròn sao cho \[\widehat {DAB} = 50^\circ \]. Gọi \[E\] là điểm đối xứng với \[A\] qua \[D\]. Số đo góc \[AEB\] bằng
Cho tam giác \[ABC\] có ba đỉnh nằm trên đường tròn \[\left( {O;{\rm{ }}R} \right)\], đường cao \[AH\], biết \[AB = 12{\rm{ cm}}\], \[AC = 15\,\,{\rm{cm}}\], \[AH = 6\,\,{\rm{cm}}\]. Đường kính của đường tròn \[\left( O \right)\] bằng
Cho \[ABC\] nhọn có ba đỉnh nằm trên đường tròn \[\left( O \right)\] đường kính \(BD\). Vẽ tia \[Bx\] sao cho tia \(BC\) nằm giữa hai tia \(Bx,\,\,BD\) và \(\widehat {xBC} = \widehat {A\,}\). Số đo góc \(\widehat {OBx}\) là