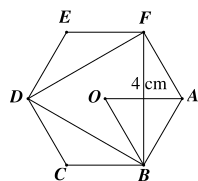
Cho lục giác đều \[ABCDEF\] tâm \(O\) biết \[OA = 4{\rm{ cm}}.\] Độ dài mỗi cạnh của lục giác đều \[ABCDEF\] là bao nhiêu?
A. \[8{\rm{ cm}}.\]
B. \[5{\rm{ cm}}.\]
C. \[4{\rm{ cm}}.\]
D. \[2{\rm{ cm}}.\]
Giải bởi Vietjack
Đáp án đúng là: C
Tổng 6 góc của lục giác đều \[ABCDEF\] bằng tổng các góc trong hai tứ giác \[ABCD\] và \[ABEF.\]
Suy ra tổng 6 góc của lục giác đều \[ABCDEF\] bằng \[2 \cdot 360^\circ = 720^\circ .\]
Do tất cả các góc của lục giác đều bằng nhau nên số đo mỗi góc của lục giác đều bằng \[\frac{{720^\circ }}{6} = 120^\circ .\]
Ta có \[AF = AB\] (vì \[ABCDEF\] là lục giác đều) và \[OB = OF\] (vì \[O\] là tâm của lục giác đều \[ABCDEF).\]
Suy ra \[AO\] là đường trung trực của đoạn BF.
Vì \[AF = AB\] (chứng minh trên) nên tam giác \[ABF\] cân tại \[A.\]
Do đó \[AO\] vừa là đường trung trực, vừa là đường phân giác của tam giác \[ABF.\]
Vì vậy \[\widehat {OAB} = \frac{{\widehat {BAF}}}{2} = \frac{{120^\circ }}{2} = 60^\circ .\]
Ta có \[OB = OA = 4{\rm{ cm}}\] (vì \[O\] là tâm của lục giác đều \[ABCDEF).\]
Suy ra tam giác \[OAB\] cân tại O, mà \[\widehat {OAB} = 60^\circ \] (chứng minh trên).
Do đó tam giác \[OAB\] đều, suy ra \[AB = OB = OA = 4{\rm{ cm}}.\]
Vì vậy \[BC = CD = DE = EF = FA = AB = 4{\rm{ cm}}\] (vì \[ABCDEF\] là lục giác đều).
Vậy số đo mỗi cạnh của lục giác đều \[ABCDEF\] đều bằng nhau và bằng \[4{\rm{ cm}}.\]
Cho tứ giác \[ABCD\] nội tiếp một đường tròn \[\left( O \right)\]. Biết \(\widehat {BOD} = 140^\circ \). Số đo góc \(\widehat {BCD}\) là
II. Thông hiểu
Phép quay với \[O\] là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc:
Khi tứ giác \[MNPQ\] nội tiếp đường tròn, và có \(\widehat M = 90^\circ \). Khi đó, góc \[P\] bằng
Cho đường tròn \[\left( O \right)\]. Trên \[\left( O \right)\] lấy ba điểm \[A,{\rm{ }}B,{\rm{ }}D\] sao cho \(\widehat {AOB} = 120^\circ \), \[AD = BD\]. Khi đó tam giác \[ABD\] là
Cho tam giác \[ABC\] có ba góc nhọn, đường cao \[AH\] và nội tiếp đường tròn tâm \[\left( O \right)\], đường kính \[AM\]. Gọi \[N\] là giao điểm của \[AH\] với đường tròn \[\left( O \right)\]. Tứ giác \[BCMN\] là
Cho tam giác \[ABC\] nhọn nội tiếp \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\]. Khẳng định nào sau đây là đúng?
III. Vận dụng
Tứ giác \[ABCD\] nội tiếp đường tròn có hai cạnh đối \[AB\] và \[CD\] cắt nhau tại \[M\] và \(\widehat {BAD} = 70^\circ \). Số đo \(\widehat {BCM}\) là
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
