Cho tam giác đều \[ABC\] có tâm \[O\] và các đường cao \[AA',BB',CC'\]. Phép quay thuận chiều tâm \[O\] góc \(240^\circ \) biến đường cao \[AA'\] thành
A. \[AA'\].
B. \[BB'\].
C. \[CC'\].
D. \[BC\].
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
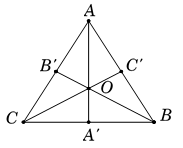
Do tam giác \[ABC\] đều nên \(\widehat {A'OB'} = \widehat {B'OC'} = \widehat {C'OA'} = 120^\circ \).
Khi đó xét phép quay tâm \[O\] góc quay \(240^\circ \):
Biến \[A\] thành \[B\] .
Biến \[A'\] thành \[B'\].
Vậy phép quay thuận chiều tâm \[O\] góc \(240^\circ \) biến đường cao \[AA'\] thành \[BB'\].
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Phép quay thuận chiều tâm \[O\] biến điểm \[A\] thành điểm \[E\] thì điểm \[C\] biến thành điểm
III. Vận dụng
Cho tam giác \[ABC\] đều nội tiếp đường tròn \[\left( O \right).\] Các phép quay giữ nguyên tam giác \[ABC\] là
Với một phép quay góc \(\alpha \) thì \(\alpha \) có thể nhận các giá trị:
II. Thông hiểu
Cho hình vuông tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến hình vuông trên thành chính nó là
I. Nhận biết
Các phép quay có thể có với một đa giác đều tâm \[O\] là
Khi quay thuận chiều \(\alpha ^\circ \) tâm \[O\] điểm \[A\] thành điểm \[B\] thì điểm \[A\] tạo thành cung \[AB\] có số đo bằng
Cho tam giác đều tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến tam giác trên thành chính nó là
Cho tam giác đều \[ABC\]. Góc quay của phép quay thuận chiều tâm A biến B thành C là
Số điểm biến thành chính nó qua phép quay tâm \[O\] góc \(\alpha \) với \(\alpha < 360^\circ \) là
Cho tam giác \[ABC\] vuông tại \[B\] và góc tại \[A\] bằng \(60^\circ \). Về phía ngoài tam giác vẽ tam giác đều \[ACD\]. Phép quay tâm \[A\] góc \(60^\circ \) biến \[BC\] thành
Cho hình chữ nhật tâm \[O\]. Số phép quay tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến hình chữ nhật trên thành chính nó là
Cho hình thoi \[ABCD\] có góc \(\widehat {ABC} = 60^\circ \). Phép quay thuận chiều tâm \[A\] một góc \(60^\circ \) biến cạnh \[CD\] thành