Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là \(5{\rm{ cm}}\). Chu vi đa giác đều này là
A. 45 cm.
B. 50 cm.
C. 60 cm.
D. 55 cm.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Chu vi đa giác đều 11 cạnh đã cho là: \(11.5 = 55{\rm{ }}\left( {{\rm{cm}}} \right)\).
Với một phép quay góc \(\alpha \) thì \(\alpha \) có thể nhận các giá trị:
I. Nhận biết
Cho các hình dưới đây:
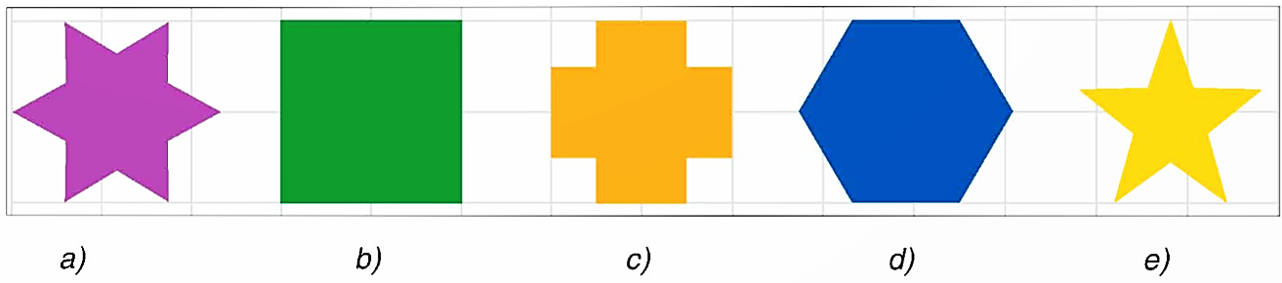
Trong các hình trên, hình nào có dạng là đa giác đều?
I. Thông hiểu
Mỗi góc của bát giác đều nội tiếp đường tròn tâm \[O\] có số đo là
Cho hình vuông tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến hình vuông trên thành chính nó là
Cho tam giác đều tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến tam giác trên thành chính nó là
Cho hình thoi \[ABCD\] có góc \(\widehat {ABC} = 60^\circ \). Phép quay thuận chiều tâm \[A\] một góc \(60^\circ \) biến cạnh \[CD\] thành
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Phép quay thuận chiều tâm \[O\] biến điểm \[A\] thành điểm \[E\] thì điểm \[C\] biến thành điểm
III. Vận dụng
Cho lục giác đều \[ABCDEF\] tâm \[O.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[EF,{\rm{ }}BD.\] Khẳng định nào sau đây là sai?
Một lục giác đều và một ngũ giác đều chung cạnh \[AD\] (như hình vẽ).
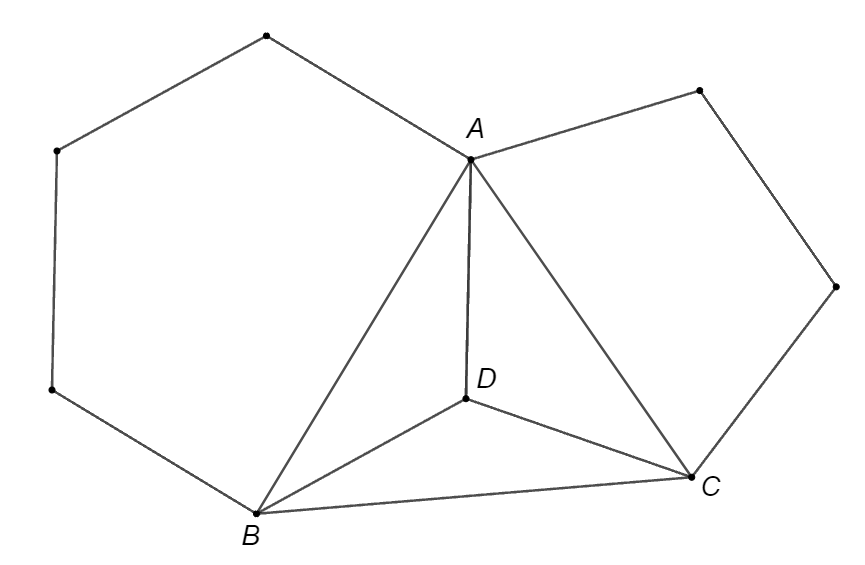
Số đo góc \(BAC\) là
Cho bát giác đều \[ABCDEFGH\] có tâm \[O.\] Phép quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm nào?
Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.
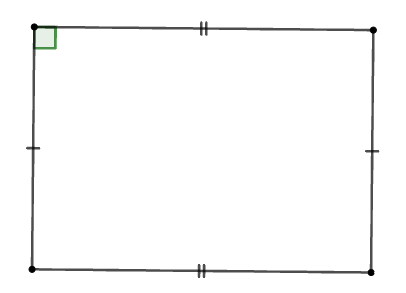
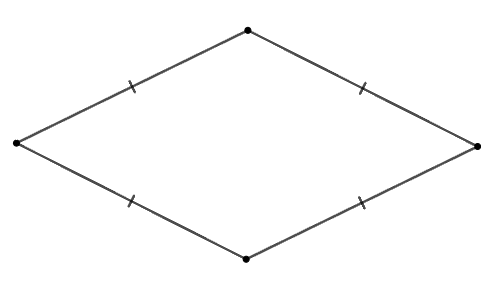
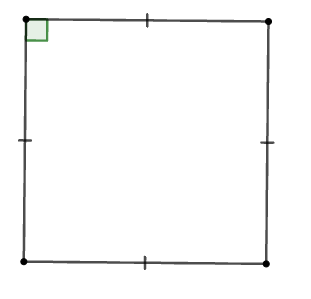
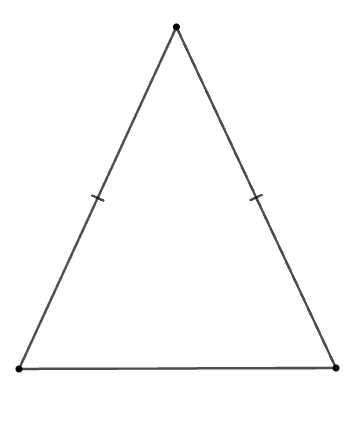
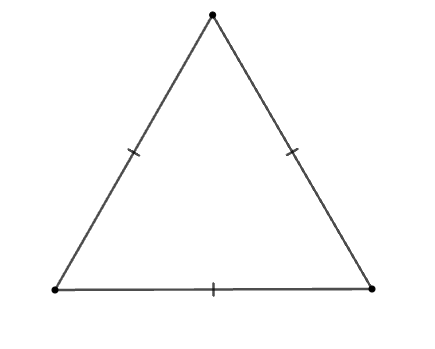
Trong các hình trên, có bao nhiêu đa giác giác đều?