Cho bảng số liệu dưới đây về thời gian (phút) tập thể dục buổi sáng của hai bạn Bình và Chi trong 30 ngày.
|
Thời gian
|
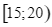
|
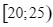
|
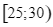
|
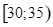
|
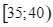
|
|
Bạn Bình
|
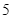
|
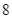
|
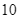
|
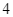
|
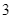
|
|
Bạn Chi
|
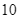
|
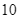
|
|
|
|
a) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục của Chi là 25 (phút).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là: 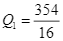 .
.
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Chi là 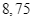 .
.
d) Phương sai của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là 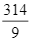 .
.
 Giải bởi Vietjack
Giải bởi Vietjack