Trong không gian với hệ tọa độ Oxyz mặt phẳng $\left(\alpha \right)$  chứa trục Oz và đi qua điểm P(2;-3;5) có phương trình là

Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của hình lập phương đơn vị để thu được một tam giác đều?

Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 5 viên bi sao cho có đủ cả ba màu. Số cách chọn là

Cho phương trình $m.9^x-\left(2m+1\right)6^x+m.4^x\le 0$.  Tìm tất cả các giá trị của tham số m để bất phương trình nghiệm đúng với mọi x thuộc (0;1]

Cho dãy số $\left(u_n\right)$  với $u_n=\frac{4n^2+n+2}{a{n}^2+5}$.  Để dãy số đã cho có giới hạn bằng 2, giá trị của a là

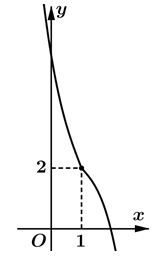
Cho hàm số y = f(x) có đạo hàm trên $\mathrm{ℝ}$  và không có cực trị, đồ thị của hàm số  y = f(x) là đường cong ở hình vẽ bên. Xét hàm số $h\left(x\right) = \frac{1}{2}{\left[f\left(x\right)\right]}^2-2xf\left(x\right)+2x^2$.  Mệnh đề nào sau đây đúng?

Một ô tô đang đi với vận tốc lớn hơn 72 km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là 72 km/h vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc $v\left(t\right) = 30 - 2t \left(m/s\right)$ trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72 km/h ô tô đã di chuyển quãng đường là bao nhiêu mét?

Cho a, b là các số thực dương thỏa ${\log }_{4}a+{\log }_4{b}^2 = 5$ và ${\log }_4{a}^2+{\log }_{4}b = 7$ thì tích ab nhận giá trị bằng

Số hạng thứ k+1 trong khai triển nhị thức ${\left(2+x\right)}^n$  là 

Biết rằng phương trình ${2018}^{x^2-12x+1} = 2019$  có hai nghiệm phân biệt $x_1, x_2$ . Tổng $x_1\hspace{0.17em}+ x_2$ bằng 

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M,N lần lượt là trung điểm SC và AD. Góc giữa đường thẳng MN và đáy (ABCD) bằng

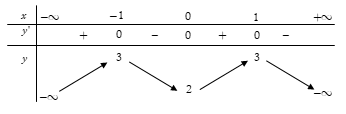
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?

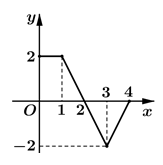
Cho hàm số $y=f\left(x\right)$ liên tục trên $\left[0;4\right]$ và có đồ thị như hình bên. Tích phân ${\int }_0^{4}f\left(x\right)dx$  bằng

Khai triển và rút gọn đa thức $P\left(x\right)={\left(2x-1\right)}^{1000}$  ta được $P\left(x\right)=a_{1000}{x}^{1000}+a_{999}{x}^{999}+...+a_{1}x+a_0$

Khẳng định nào sau đây là đúng?

Số lượng của loại vi khuẩn A trong một phòng thí nghiệm ước tính theo công thức $S_t=S_0.2^t$  trong đó  là số lượng vi khuẩn A ban đầu, $S_t$  là số lượng vi khuẩn A có sau  phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?

Tìm m để hàm số y = $\frac{\cos x}{\sqrt{3\sin 5x-4\cos 5x-2m+3}}$ có tập xác định là  $\mathrm{ℝ}$