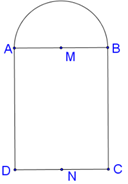
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
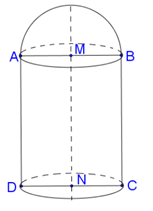
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn , có thể tích ;
- nửa hình cầu tâm M bán kính MA, có thể tích
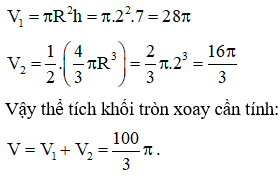
Tiếp tuyến của đồ thị hàm số tại điểm cực tiểu của đồ thị có phương trình
Giả sử là các nghiệm phức của phương trình . Giá trị của biểu thức là
Trong không gian cho đường thẳng d có phương trình . Một véctơ chỉ phương của d là
Cho hình lăng trụ đứng tam giác , tam giác ABC có , góc , . Tính thể tích khối lăng trụ là
Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4.