Ông Minh gửi tiết kiệm 100 triệu đồng theo hình thức lãi kép với lãi suất không đổi là 0,7% một tháng. Do nhu cầu cần chi tiêu, cứ mỗi tháng sau đó (kể từ khi gửi tiết kiệm), ông rút ra 2 triệu đồng từ số tiền của mình. Hỏi cứ như vậy thì tháng cuối cùng ông Minh rút nốt được bao nhiêu triệu đồng?
A. 0,9087.
B. 1,1105.
C. 1,3142.
D. 1,5019.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Tổng quát:
Gọi A là sô tiền ban đầu ông Minh gửi (triệu đồng);
r: lãi suất/một tháng.a: số tiền mỗi tháng ông rút ra (triệu đồng);
- Sau tháng đầu tiên, số tiền cả gốc lẫn lãi ông Minh nhận được là A(1+r)
Ông rút ra a triệu đồng, số tiền còn lại là A(1+r)-a
- Sau tháng thứ hai, số tiền cả gốc lẫn lãi là ![]()
Rút ra a triệu đồng, số tiền còn lại là
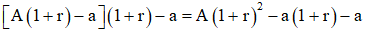
- Sau tháng thứ 3, sau khi rút ra a triệu đồng, số tiền còn lại là:
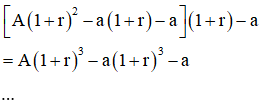
- Sau tháng thứ n, sau khi rút ra a triệu đồng, số tiền còn lại:

Giả sử sau n tháng, ông Minh rút hết số tiền, tức là:
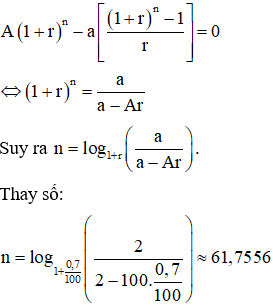
Như vậy, sau 61 tháng rút tiền thì số tiền còn lại trong tháng cuối cùng (tháng thứ 62) là:

Cho hàm số và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ là
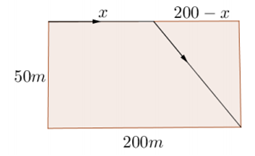
Có một cái hồ rộng 50m, dài 200m. Một vận động viên chạy phối hợp với bơi (bắt buộc cả hai) cần đi từ góc này qua góc đối diện bằng cách cả chạy và bơi (như hình vẽ). Hỏi rằng sau khi chạy được bao xa (quãng đường x) thì nên nhảy xuống bơi để đến đích nhanh nhất? Biết rằng vận tốc bơi là 1,5 m/s và vận tốc chạy là 4,5 m/s.
Trong không gian cho tam giác ABC vuông tại B, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
Một ca nô đang chạy trên biển với tốc độ thì hết xăng. Từ thời điểm đó, ca nô chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc hết xăng. Hỏi từ lúc hết xăng đến khi dừng hẳn, ca nô đi được bao nhiêu mét?
Trong không gian cho tam giác ABC vuông tại B, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
Trong không gian tọa độ Oxyz, cho mặt cầu và . Tìm các giá trị của m để tiếp xúc với .
Viết phương trình tiếp tuyến của đồ thị hàm số . Biết tiếp tuyến tạo với trục hoành một góc .
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số không có tiệm cận đứng.
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và đường thẳng .
Diện tích hình phẳng giới hạn bởi đồ thị hàm số liên tục trên , trục hoành và hai đường thẳng được tính theo công thức nào sau đây?
Cho hàm số và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ là