Cho phương trình $4^{-\left|x-a\right|}.{\log }_{\sqrt{3}}\left(x^2-2x+3\right)+2^{-x^2+2x}.{\log }_{\frac{1}{3}}\left(2\left|x-a\right|+2\right)=0$. Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm $x_1;x_2;x_3;x_4$ thỏa mãn là (c;d). Khi đó giá trị biểu thức $T=2c+2d$ bằng: 

Họ nguyên hàm của hàm số $f\left(x\right)=\cos x$ là 

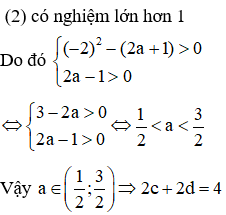
Cho hình trụ có hai đường tròn đáy là (O) và (O'). Gọi A trên đường tròn ( O) và B trên đường tròn (O') sao cho AB = 4a. Biết khoảng cách từ đường thẳng AB đến trục của hình trụ a là OO'=2a. Tính diện tích xung quanh của hình trụ đã cho 

Cho các số dương a, b, c thỏa mãn $2^a=6^b={12}^c$.Khi đó biểu thức $T=\frac{b}{c}-\frac{b}{a}$ có giá trị là 

Cho hàm số f(x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn

$x+2xf\left(x\right)={\left[f\text{'}\left(x\right)\right]}^2, \forall x\in \left[1;4\right], f\left(1\right)=\frac{3}{2}$. Giá trị f(4) bằng:

Cho hàm số $y=x^3-12x+12$có đồ thị (C) và điểm A(m;-4). Gọi S là tập hợp tất cả các giá trị thực của m nguyên thuộc khoảng (2;5) để từ A kẻ được ba tiếp tuyến với đồ thị (C). Tổng tất cả các phần tử nguyên của S bằng 

Đạo hàm của hàm số $y={\log }_3\left(4x+1\right)$ là

Cho a > 0, b > 0 và x, y là các số thực bất kỳ. Đẳng thức nào sau đây đúng?

Cho các số thực x và y thỏa mãn các điều kiện $2^{2x+7y}=256$ và ${\log }_{\sqrt{3}}\left(6y+11x\right)=2$.Tính trung bình cộng của x và y

Trong không gian Oxyz, cho điểm M (1;2;0) và hai đường thẳng ${∆}_1: \left\{\begin{array}{l}x=1+2t\\ y=2-2t\\ z=-1+t\end{array}\right.\left(t\in \mathrm{ℝ}\right)$, ${∆}_2: \left\{\begin{array}{l}x=3+2s\\ y=-1-2s\\ z=s\end{array}\right.\left(s\in \mathrm{ℝ}\right)$. Mặt phẳng (P) đi qua M song song với trục Ox, sao cho (P) cắt hai đường thẳng ∆_1; ∆₂ lần lượt tại A, B thỏa mã AB =1. Khi đó mặt phẳng (P) đi qua điểm nào trong các điểm có tọa độ sau

Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng $\left(P\right): x+\sqrt{2}y-z+3=0$ cắt mặt cầu $\left(S\right):\hspace{0.17em}{x}^2+y^2+z^2=5$ theo giao tuyến là đường tròn có diện tích là

Giả sử x; y là các số thực dương. Mệnh đề nào sau đây sai?

Cho f(x), g(x) là các hàm liên tục trên R. Chọn khẳng định sai trong các khẳng định sau đây

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?

Cho hình chóp S.ABC có tam giác ABC vuông tại A, $AB=2a,AC=a, SA=3a, SA\perp \left(ABC\right)$. Thể tích của hình chóp là 

Từ 10 điểm trong một mặt phẳng mà với 3 điểm bất kì không thẳng hàng có thể tạo thành bao nhiêu tam giác?