Cho tập số Tập nghiệm của bất phương trình f'(x)≤0 là:
A. (-∞;2)∪[2;+∞)
B. (-∞;2)
C. [2;+∞)
D. (2;+∞)
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
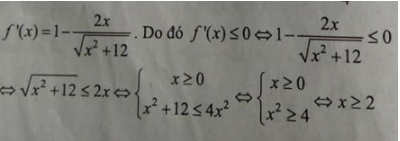
Đạo hàm của hàm số (với a là hằng số) bằng biểu thức nào sau đây?