Cho hàm số $y=a{x}^3+b{x}^2+cx+d$ có đồ thị như hình bên.

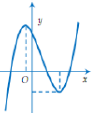
Khẳng định nào sau đây đúng?

Tính đạo hàm của hàm số sau: $f\left(x\right)=\ln \left(x^2+1\right)$

Giá trị lớn nhất của hàm số $y=x\left(2-\ln x\right)$ trên đoạn $\left[2;3\right]$là

Cho hàm số $y=x^3-3m{x}^2+6,$ giá trị nhỏ nhất của hàm số trên $\left[0;3\right]$ bằng 2 

Cho a, b, c là ba số thực dương, khác 1 và $abc\ne 1$. Biết ${\log }_{a}3=2,{\log }_{b}3=\frac{1}{4}$và ${\log }_{abc}3=\frac{2}{15}.$ Khi đó, giá trị của ${\log }_{c}3$ bằng bao nhiêu? 

Cho hàm số $y=f\left(x\right)$ xác định, liên tục và có đạo hàm trên đoạn $\left[a,b\right].$ Xét các khẳng định sau:

1. Hàm số $f\left(x\right)$ đồng biến trên $\left(a;b\right)$ thì $f\text{'}\left(x\right)>0,\forall x\in \left(a;b\right)$

2. Giả sử $f\left(a\right)>f\left(c\right)>f\left(b\right),\forall x\in \left(a;b\right)$ suy ra hàm số nghịch biến trên $\left(a;b\right)$

3. Giả sử phương trình $f\text{'}\left(x\right)=0$ có nghiệm là $x=m$ khi đó nếu hàm số $y=f\left(x\right)$ đồng biến trên $\left(m;b\right)$ thì hàm số $y=f\left(x\right)$ nghịch biến trên $\left(a,m\right)$

4. Nếu $f\text{'}\left(x\right)\ge 0,\forall x\in \left(a;b\right)$, thì hàm số đồng biến trên $\left(a;b\right)$

Số khẳng định đúng trong các khẳng định trên là

Đồ thị hàm số $y=\frac{\sqrt{x^2-x+2-2}}{x^2-1}$ có bao nhiêu đường tiệm cận đứng? 

Cho hàm số $y=\frac{3x}{1+2x}$ . Khẳng định nào sau đây là khẳng định đúng ?

Phương trình $m\sin x+3\cos x=5$ có nghiệm khi và chỉ khi

Cho tam giác ABC vuông tại A, AB=a, BC=2a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC.

Cho khối chóp S.ABC có thể tích là $\frac{a^3}{3}$. Tam giác SAB có diện tích là $2a^2$. Tính khoảng cách d từ C đến mặt phẳng (SAB). 

Tập hợp tất cả các giá trị của m để hàm số $y=\frac{1}{3}{x}^3-\left(m-1\right)x^2+2\left(m-1\right)x-2$ luôn tăng trên R

Tìm m để phương trình sau có nghiệm:

$\sqrt{3+x}+\sqrt{6-x}-\sqrt{\left(3+x\right)\left(6-x\right)}=m$

Cho phương trình:

$(m -1){\log }_{\frac{1}{2}}^2{\left(x-2\right)}^2+4\left(m-5\right){\log }_{\frac{1}{2}}\frac{1}{x-2}+4m-4=0$ (với m là tham số). Gọi $S= [a;b]$ là tập các giá trị của m để phương trình có nghiệm trên đoạn $\left[\frac{5}{2};4\right]$. Tính a+b.

Trong các hàm số sau, hàm số nào nghịch biến trên khoảng $\left(0;\sqrt{2}\right)$

Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 7,4%/năm. Biết rằng nếu không rút tiền ra khỏi ngan hàng thì cứ sau mỗi năm, số tiền sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Để lãnh được số tiền ít nhất 250 triệu thì người đó cần gửi trong khoảng thời gian bao nhiêu năm? (nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi)