Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB, O là điểm bất kì. Khẳng định nào sau đây là đúng nhất?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án D
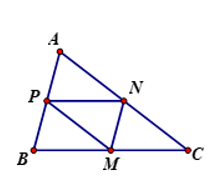
Theo quy tắc ba điểm ta có:

Trong mặt phẳng tọa độ Oxy, cho ba điểm A (6; 3), B (−3; 6), C (1; −2). Gọi điểm D trên trục hoành sao cho ba điểm A, B, D thẳng hàng, điểm E thuộc đoạn BC sao cho BE = 2EC. Xác định giao điểm hai đường thẳng DE và AC.
Trong mặt phẳng tọa độ Oxy cho A (3; −1), B (−1; 2) và I (1; −1). Gọi C, D là các điểm sao cho tứ giác ABCD là hình bình hành, biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD.
Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất biết A(1;2) và B(3;4)
Cho hình bình hành ABCD có A (−2; 3) và tâm I (1; 1). Biết điểm K (−1; 2) nằm trên đường thẳng AB và điểm D có hoành độ gấp đôi tung độ. Chọn kết luận đúng:
Cho hình bình hành ABCD có AD = 4 và chiều cao ứng với cạnh AD = 3, . Chọn hệ trục tọa độ sao cho và cùng hướng, yB > 0. Tìm khẳng định sai?
Cho hình thoi ABCD cạnh a và . Gọi O là tâm hình thoi. Chọn kết luận đúng?
Cho hình vuông ABCD có tâm là O và cạnh a. M là một điểm bất kỳ. Chứng minh rằng không phụ thuộc vị trí điểm M. Tính độ dài vectơ
Cho tam giác ABC có A (3; 4), B (2; 1), C(−1; −2). Tìm điểm M trên đường thẳng BC sao cho