Cho $\overrightarrow{a}=\left(1;3\right),\overrightarrow{b}=\left(-3;0\right),\overrightarrow{c}=\left(-1;2\right)$. Phân tích vec tơ $\overrightarrow{c}$ qua  $\overrightarrow{a},\overrightarrow{b}$

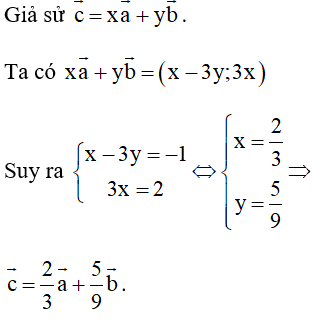
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A (0; 3), D (2; 1) và 

I (−1; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC.

Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của AG. Tính độ dài của vectơ  $\overrightarrow{BI}$

Cho tam giác ABC có trọng tâm G. Gọi I là trung điểm của BC. Dựng điểm B’ sao cho $\overrightarrow{B\text{'}B}=\overrightarrow{AG}$ , gọi J là trung điểm của BB’. Khẳng định nào sau đây là đúng?

Tam giác ABC là tam giác nhọn có AA’ là đường cao

Khi đó vec tơ $\overrightarrow{u}=\left(\tan B\right)\overrightarrow{A\text{'}B}+\left(\tan C\right)\overrightarrow{A\text{'}C}$ là:

Trong hệ tọa độ Oxy, cho ba điểm A (0; −3), B (2; 1), D (5; 5) Tìm tọa độ điểm C để tứ giác ABCD là hình bình hành.

Cho hình thang ABCD có đáy AB = a, CD = 2a. Gọi M, N lần lượt là trung điểm AD và BC. Tính độ dài của vec tơ  $\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}$

Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB.

Biết M (1; 1), N (−2; −3), P (2; −1). Chọn đáp án đúng nhất:

Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Độ dài vec tơ $\overrightarrow{MN}$ là:

Cho ΔABC. Tìm tập hợp các điểm M sao cho:   $\left|\overrightarrow{MA}+3\overrightarrow{MB}-2\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|$

Trên mặt phẳng tọa độ Oxy, cho  vuông tại A có B(1;-3) và C(1;2). Tìm tọa độ điểm H là chân đường cao kẻ từ đỉnh A của $∆ABC$, biết AB = 3, AC = 4

Cho tam giác ABC, M và N là hai điểm thỏa mãn: $\overrightarrow{BM}=\overrightarrow{BC}-2\overrightarrow{AB}$, $\overrightarrow{CN}=x\overrightarrow{AC}-\overrightarrow{BC}$. Xác định x để A, M, N thẳng hàng

Cho tứ giác ABCD trên cạnh AB, CD lần lượt lấy các điểm M, N sao cho $3\overrightarrow{AM}=2\overrightarrow{AB}$

 và $3\overrightarrow{DN}=2\overrightarrow{DC}$. Tính vec tơ $\overrightarrow{MN}$ theo hai vec tơ  $\overrightarrow{AD},\overrightarrow{BC}$

Tam giác ABC thỏa mãn: $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AC}\right|$  thì tam giác ABC là

Cho hai vec tơ $\overrightarrow{a}$ và $\overrightarrow{b}$ thỏa mãn các điều kiện $\left|\overrightarrow{a}\right|=1;\left|\overrightarrow{b}\right|=2;\left|\overrightarrow{a}-2\overrightarrow{b}\right|=\sqrt{15}$. Đặt $\overrightarrow{u}=\overrightarrow{a}+\overrightarrow{b}$

 và $\overrightarrow{v}=2k\overrightarrow{a}-\overrightarrow{b}$, k$\in R$ . Tìm tất cả các giá trị của k sao cho  $\left(\overrightarrow{u},\overrightarrow{v}\right)={60}^0$

Cho hai lực $\overrightarrow{F_1}=\overrightarrow{MA}, \overrightarrow{F_2}=\overrightarrow{MB}$ cùng tác động vào một vật tại điểm M cường độ hai lực  lần lượt là: 300 (N) và 400 (N).$\widehat{AMB}={90}^0$ . Tìm cường độ của lực tổng hợp tác động vào vật.