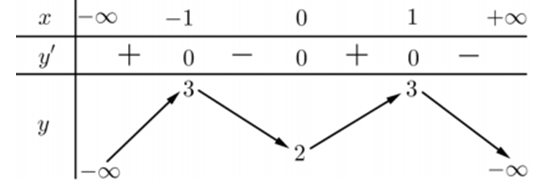
Trong bốn hàm số được liệt kẻ ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
Hàm số đã cho là hàm bậc bốn trùng phương có dạng .
- Dựa vào nhánh cuối cùng của đồ thị hàm số suy ra dấu của hệ số ![]() và loại đáp án.
và loại đáp án.
- Dựa vào giao điểm của đồ thị với trục tung suy ra hệ số c và loại đáp án.
Giải chi tiết:
Hàm số đã cho là hàm bậc bốn trùng phương có dạng .
Vì nhánh cuối cùng của đồ thị đi xuống nên Loại đáp án A và C.
Vì đồ thị hàm số đi qua điểm nên Loại đáp án B và chọn đáp án D.
Đáp án D
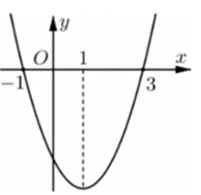
Cho hàm số có đồ thị là parabol như hình vẽ bên. Khẳng định nào sau đây là đúng?
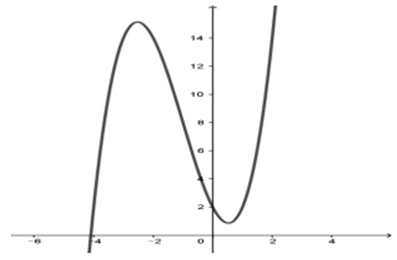
Cho hàm số bậc ba có đồ thị là đường cong như hình vẽ bên. Hỏi phương trình có bao nhiêu nghiệm phân biệt.
Cho hình chóp có đáy là hình chữ nhật với . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng .
Có bao nhiêu số tự nhiên có 4 chữ số khác nhau và khác 0 mà trong mỗi số luôn có mặt hai chữ số chẵn là hai chữ số lẻ?
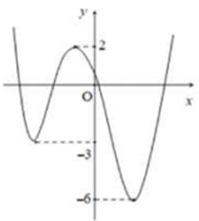
Cho hàm số là hàm đa thức bậc bốn có đồ thị như hình vẽ bên. Hỏi có bao nhiêu giá trị của tham số m thuộc đoạn để hàm số có đúng 5 điểm cực trị?
Tính tổng các giá trị nguyên của tham số m trên để hàm số nghịch biến trên khoảng .
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng sau?
Cho các số thực thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tổng bằng: