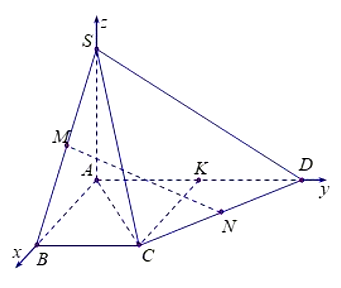
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B và có AB = BC = a, AD = 2a có SA vuông góc với đáy và SA = a. Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin của góc giữa MN và (SAC)
A. .
B. .
C. .
D. .
Giải bởi Vietjack
Chọn hệ trục tọa độ như hình vẽ.
Khi đó
Do M, N lần lượt là trung điểm của SB, CD nên M, N có tọa độ lần lượt là:
là vectơ chỉ phương của đường thẳng MN.
Gọi K là trung điểm của là hình bình hành.
Suy ra: Tam giác ACD vuông tại C.
Ta có
Mà: là vectơ pháp tuyến của .
Gọi là góc giữa MN và .
Ta có:
Chọn A.
Bất phương trình có tập nghiệm là (a;b). Tính giá trị của S = a + b.
Có bao nhiêu giá trị nguyên của tham số sao cho hàm số nghịch biến trên khoảng ?
Các mặt của một con súc sắc được đánh số từ 1 đến 6. Người ta gieo con súc sắc 3 lần liên tiếp và nhân các con số nhận được trong mỗi lần gieo với nhau. Tính xác suất để tích thu được là một số chia hết cho 6.
Cho hàm số y = f(x) có bảng biến thiên như sau
Số nghiệm của phương trình f(x) = 0 là
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và đường thẳng Viết phương trình đường thẳng đi qua A(1;-1;2) đồng thời vuông góc với cả hai đường thẳng d1 và d2.
Cho hàm số có bảng xét dấu đạo hàm như sau:
Hàm số có bao nhiêu điểm cực trị?
Một người gửi tiết kiệm 50 triệu đồng vào một ngân hàng với lãi suất 7% một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu và lãi suất không đổi trong các năm gửi. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi gần với số nào nhất?
