Cho hình chóp \(S.ABCD\) có \(SA = a,SA \bot \left( {ABCD} \right),\) đáy \(ABCD\) là hình vuông. Gọi \(M\) là trung điểm của \(AD,\) góc giữa \(\left( {SBM} \right)\) và mặt đáy bằng \({45^0}.\) Tính khoảng cách từ \(D\) đến mặt phẳng \(\left( {SBM} \right).\)
A.\(\frac{{a\sqrt 2 }}{2}.\)
B.\(\frac{{a\sqrt 3 }}{2}.\)
C.\(a\sqrt 2 .\)
D.\(\frac{{a\sqrt 2 }}{3}.\)
 Giải bởi Vietjack
Giải bởi Vietjack
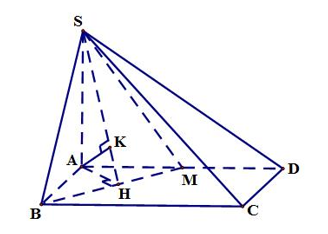
Ta có:
\(\left( {SBM} \right) \cap \left( {ABCD} \right) = BM\)
Kẻ \(AH \bot BM \Rightarrow \) Góc giữa (SBM) và mặt đáy là \(\widehat {SHA}\) và \(\widehat {SHA} = {45^0}.\)
Do đó \(\Delta SAH\) là tam giác vuông cân, \(SH = a\sqrt 2 .\)
Kẻ \(AK \bot SH \Rightarrow d\left( {A,\left( {SBM} \right)} \right) = AK = \frac{{a\sqrt 2 }}{2}.\)
Vì \(M\) là trung điểm của \(AD\) nên \(d\left( {D,\left( {SBM} \right)} \right) = d\left( {A,\left( {SBM} \right)} \right) = \frac{{a\sqrt 2 }}{2}\)
Đáp án A.
Cho khối tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc và \(OA = 3cm,OB = 4cm,OC = 10cm.\) Thể tích khối tứ diện \(OABC\) bằng
Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) (\(m\) là tham số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = \frac{{16}}{3}.\) Mệnh đề nào dưới đây đúng?
Có tất cả bao nhiêu số nguyên dương \(m\) để hàm số \(y = \frac{{\cos x + 1}}{{10\cos x + m}}\) đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ.
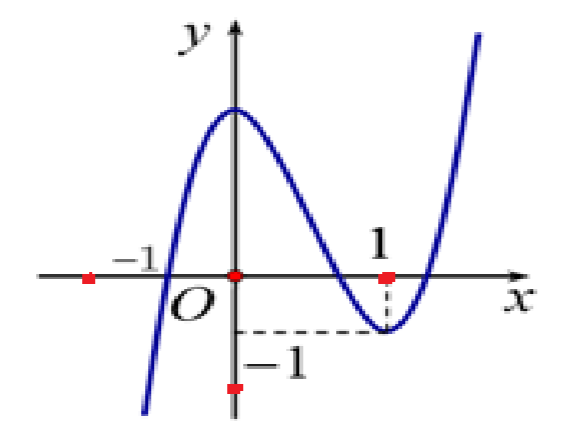
Hàm số \(y = f\left( {\left| {x + 1} \right| - 1} \right)\) có bao nhiêu điểm cực trị?
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^2} - x + 5\) biết tiếp tuyến đó vuông góc với đường thẳng \(y = - \frac{1}{3}x + 1.\)
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(ABC,SA = 1\) và đáy \(ABC\) là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng \(SBC\) và mặt phẳng \(ABC.\)
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên.
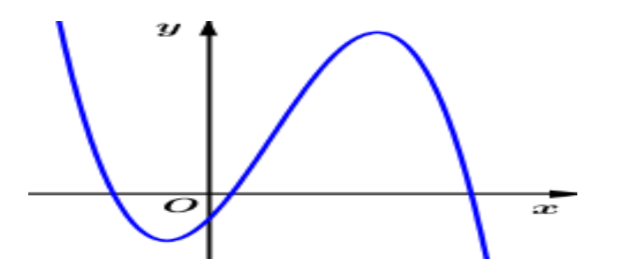
Trong các giá trị \(a,b,c,d\) có bao nhiêu giá trị âm?
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Biết \(f\left( 2 \right) + f\left( 6 \right) = 2f\left( 3 \right).\) Tập nghiệm của phương trình \(f\left( {{x^2} + 1} \right) = f\left( 3 \right)\) có số phần tử bằng
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Thể tích khối lăng trụ tam giác đều đã cho bằng
Cho khối chóp tam giác đều có cạnh đáy bằng 2 và chiều cao \(h = 12.\) Thể tích của khối chóp đã cho bằng
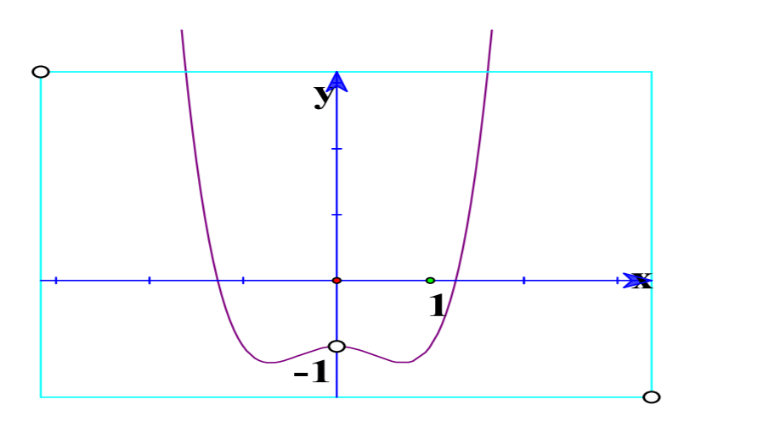
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có điểm \(O\) và \(G\) lần lượt là tâm của mặt bên \(ABB'A'\) và trọng tâm của \(\Delta ABC.\) Biết \({V_{ABC.A'B'C'}} = 270c{m^3}.\) Thể tích của khối chóp \(AOGB\) bằng