Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a.\) Trên các tia \(AA',BB',CC'\) lần lượt lấy \({A_1},{B_1},{C_1}\) cách mặt phẳng đáy \(\left( {ABC} \right)\) một khoảng lần lượt là \(\frac{a}{2},a,\frac{{3a}}{2}.\) Tính góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {{A_1}{B_1}{C_1}} \right).\)
A.\({60^0}.\)
B. \({90^0}.\)
C.\({45^0}.\)
D.\({30^0}.\)
 Giải bởi Vietjack
Giải bởi Vietjack
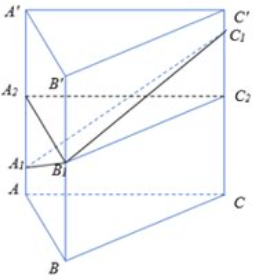
Từ \({B_1}\) dựng mặt phẳng song song với \(\left( {ABC} \right)\) cắt \(AA'\) và \(CC'\) tại \({A_2},{C_2}.\)
Ta có \({A_1}{A_2} = B{B_1} - A{A_1} = \frac{a}{2} \Rightarrow {A_1}{B_1} = \sqrt {{A_1}A_2^2 + {A_2}{B_1}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2},\) tương tự \({B_1}{C_1} = \frac{{a\sqrt 5 }}{2},{A_1}{C_1} = a\sqrt 2 .\) Vậy tam giác \({A_1}{B_1}{C_1}\) cân tại \({B_1}.\)
Khi đó đường cao ứng với đỉnh \({B_1}\) của tam giác \({A_1}{B_1}{C_1}\) là \(\sqrt {{B_1}C_1^2 - \frac{{{A_1}C_1^2}}{4}} = \frac{{a\sqrt 3 }}{2}\)
\({S_{\Delta {A_1}{B_1}{C_1}}} = \frac{{{a^2}\sqrt 6 }}{4};{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4},\) mặt khác tam giác \(ABC\) là hình chiếu của tam giác \({A_1}{B_1}{C_1}\) trên mặt phẳng \(\left( {ABC} \right).\)
Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {{A_1}{B_1}{C_1}} \right).\)
Ta có \(\cos \varphi = \frac{{{S_{\Delta ABC}}}}{{{S_{{A_1}{B_1}{C_1}}}}} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\)
Đáp án C
Có bao nhiêu giá trị nguyên âm của tham số \(m\) để hàm số \(y = {x^3} + mx - \frac{1}{{5{x^2}}}\) đồng biến trên khoảng \(\left( {0; + \infty } \right)?\)
Cho khối lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy và cạnh bên cùng bằng \(a.\) Tính thể tích của khối lăng trụ đó theo \(a.\)
Tổng giá trị tất cả các nghiệm của phương trình \({\log _3}x.{\log _9}x.{\log _{27}}x.{\log _{81}}x = \frac{2}{3}\) bằng
Với \(a,b\) là các số thực dương tùy ý và \(a \ne 1.\) Ta có \({\log _{{a^2}}}b\) bằng
Biết rằng tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \({\left( {2 + \sqrt 3 } \right)^x} + m{\left( {2 - \sqrt 3 } \right)^x} = 1\) có hai nghiệm phân biệt là khoảng \(\left( {a;b} \right).\) Tính \(T = 3a + 8b.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^2}\left( {{x^2} - 2x} \right),\) với mọi \(x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = f\left( {{x^2} - 8x + m} \right)\) có 5 điểm cực trị?
Cho khối chóp \(S.ABC\) có tam giác \(ABC\) vuông tại \(B,AB = \sqrt 3 ,BC = 3,SA \bot \left( {ABC} \right)\) và góc giữa \(SC\) với đáy bằng \({45^0}.\) Thể tích của khối chóp \(S.ABC\) bằng
Đường cong hình sau là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai \(d = 2.\) Tính \({u_9}.\)
Thể tích \(V\) của khối lăng trụ có diện tích đáy \(B\) và chiều cao \(h\) là:
Nghiệm của phương trình \({\log _2}\left( {x + 1} \right) = 3\) là:
Biết rằng \[a\] là số thực dương để bất phương trình \[{a^x} \ge 9x + 1\] nghiệm đúng với mọi \[x \in \mathbb{R}\]. Mệnh đề nào sau đây đúng?
Trong không gian \(Oxyz,\) cho hình hộp \(ABCD.A'B'C'D'\). Tìm tọa độ đỉnh \(A'\) biết tọa độ các điểm \(A\left( {0;0;0} \right);B\left( {1;0;0} \right);C\left( {1;2;0} \right);D'\left( { - 1;3;5} \right).\)
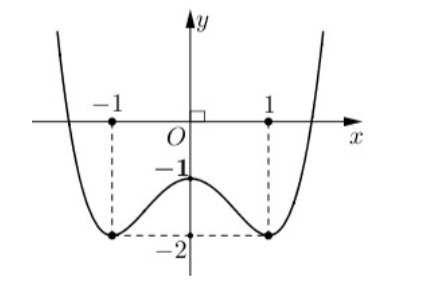
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị hình dưới đây. Hỏi phương trình \(2f\left( x \right) = - 1\) có bao nhiêu nghiệm?