Một hình chóp có đáy là tam giác đều cạnh bằng \(2\) và có chiều cao bằng \(4.\) Tính thể tích khối chóp đó.

Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên

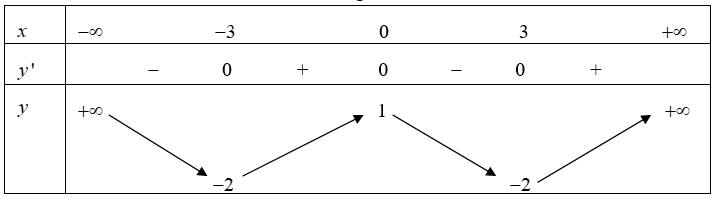
Tìm \(m\) để phương trình \(2f(x) + m = 0\) có đúng \(3\) nghiệm phân biệt

Cho hàm số \(y = {x^3} - 6{x^2} + 7x + 5\) có đồ thị là \(\left( C \right)\). Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm có hoành độ bằng 2 là:

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \[A\]. Biết \(AB = AA' = a\), \(AC = 2a\). Gọi \(M\) là trung điểm của \[AC\]. Diện tích mặt cầu ngoại tiếp tứ diện \(MA'B'C'\) bằng

Cho tứ diện \[ABCD\] có \[AC = AD = BC = BD = 1\], mặt phẳng\[\left( {ABC} \right) \bot (ABD)\] và \[\left( {ACD} \right) \bot (BCD)\]. Khoảng cách từ \[A\] đến mặt phẳng \[\left( {BCD} \right)\]là:

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(A\), \(AB = AC = a\), \(AA' = \sqrt 2 a\). Thể tích khối cầu ngoại tiếp hình tứ diện \(AB'A'C\) là

Cho tứ diện \[OABC\] có \[OA\], \[OB\], \[OC\] đôi một vuông góc nhau và \[OA = OB\]\[ = OC = 3a\]. Tính khoảng cách giữa hai đường thẳng \[AC\] và \[OB\].

Cho hàm đa thức \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ sau

Có bao nhiêu giá trị của \(m \in \left[ {0;\,6} \right];\,2m \in \mathbb{Z}\) để hàm số \(g(x) = f\left( {{x^2} - 2\left| {x - 1} \right| - 2x + m} \right)\) có đúng \(9\) điểm cực trị?

Giá trị của giới hạn \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^3} + 2{x^2} + 1}}{{{x^2} + 1}}\) là

Cho hàm số \(f(x) = - \frac{1}{3}{x^3} + m{x^2} + \left( {3m + 2} \right)x - 5\) . Tập hợp các giá trị của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\) là \(\left[ {a;\,b} \right]\). Khi đó \(2a - b\) bằng

Cho hình chóp \[S.ABCD\], đáy là hình chữ nhật tâm \[O\], \[AB = a\], \[AD = a\sqrt 3 \], \[SA = 3a\], \[SO\] vuông góc với mặt đáy \[\left( {ABCD} \right)\]. Thể tích khối chóp bằng

Số giá trị nguyên của tham số \(m\) để hàm số \(y = m{x^4} - \left( {m - 3} \right){x^2} + {m^2}\)không có điểm cực đại là

Tính thể tích \[V\] của khối lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) biết độ dài cạnh đáy của lăng trụ bằng \[2\] đồng thời góc tạo bởi \(A'C\) và đáy \[\left( {ABCD} \right)\] bằng \[30^\circ \].

Cho \(4\) số \(a,\,b,\,c,\,d\) thỏa mãn điều kiện \({a^2} + {b^2} = 4a + 6b - 9\) và \(3c + 4d = 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = {\left( {a - c} \right)^2} + {\left( {b - d} \right)^2}\) ?

Có bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau?

Hàm số \(y = \left| {{{\left( {x - 1} \right)}^3}\left( {x + 1} \right)} \right|\) có bao nhiêu điểm cực trị?